Gauss's Law and Gravity

Contents

• Example 1
• Example 2
• Example 3
• References

Introduction

An equipotential surface, like the geoid, undulates in shape because of mass heterogeneities. The gravitational potential can be reformulated to reflect the distribution of many masses: $$U= \sum_{i=1}^{N} U_i = \sum_{i=1}^{N}-\frac{G m_i}{r_i}$$ where:

• $N$ is the number of individual masses,
• $m_i$ is the $i^{th}$ mass,
• located at distance $r_i$
• $G$ is the gravitational constant.

In practice, individual masses inside the Earth are volumes, $V$, of similar density, $\rho$. It is the density contrast between masses that defines them. In the limit: $$U = -G \int_V \frac{\rho dV}{r}$$ This integral is a key part of Gauss's law, which relates the total mass of an anomalous body to the integrated gravity field produced by the body. The mass distribution is described by the above equation.

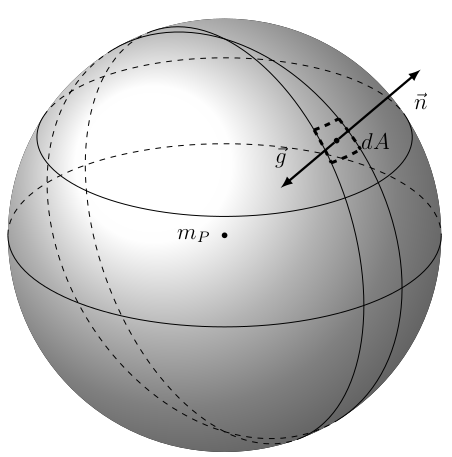
Consider any mass distribution (like the Earth); this mass distribution can be completely contained by a surface (like an equipotential surface). In the following figure, the mass is at a point and is located at $m_P$. This point's equipotential surface is drawn as the gray shaded sphere. The sum of the gravity field across the entire equipotential (gray) surface is: $$\oint_S \vec g \cdot \vec n dA$$

The contour integral symbol is shorthand indicating that the integral includes the entire surface area, which is divided into small areas, $dA$. The unit vector, $\vec n$, is normal to the surface and directed outward (away from the mass) at each $dA$.

[Top]

Example 1 of Gauss's law

A physical analogy might help. Consider a well pumping groundwater out of a thick saturated sandstone. Imagine a hypothetical surface that completely encloses the well; in a steady-state, all groundwater pumped from the well must pass through this surface. The total water pumped from the well in any given time (say one second) is equal to the amount of water passing through the hypothetical enclosing surface in the same amount of time. The field in this case is the velocity of water pulled toward the well across the surface, the potential is the pressure gradient that drives the water at this velocity, and the contour integral yields the total flux of water across the surface.

Suppose the sandstone aquifer is so uniform that a spherical surface exists, all across which the groundwater velocity is 2 m s$^{-1}$ toward the well. The surface area of this hypothetical sphere is $4 \pi r^2$, so the well must be pumping water at a rate of $8 \pi r^2$ m$^3$ s$^{-1}$. The velocity of water integrated across the entire enclosing spherical surface is equal to the flux of water from the well, regardless of the value of $r$.

For a point mass with the spherical enclosing surface located at $r$, the solution to the integral is just the surface area of the sphere multiplied by the gravity at $r$: $$ \oint_{S} \vec g \cdot \vec n dA = -4 \pi r^2 \frac{GM}{r^2} = -4 \pi G \int_V \rho dV$$.

In other words, the integral of the gravity across the entire enclosing surface is proportional to the mass enclosed by the surface, regardless of the value of $r$. This is Gauss's law. It turns out to be applicable regardless of the mass distribution within the enclosing surface, or the shape of the enclosing surface. Because we know $G$ very well, the total mass can be determined by measuring the gravity field, without knowing anything about the mass distribution. From satellites (e.g., GRACE) we can measure gravity everywhere on a surface and so determine the mass of the Earth, despite the fact that mass is heterogeneously distributed in Earth. In fact, after Cavendish estimated $G$, a big activity of geophysicists was measuring $g$ around the globe to improve estimates of the Earth's mass.

[Top]

Example 2 of Gauss's law

For a point mass with the spherical enclosing surface located at $r$, the solution to the integral is just the surface area of the sphere multiplied by the gravity at $r$: $$\oint_{S} \vec g \cdot \vec n dA = -4 \pi r^2 \frac{GM}{r^2} = -4 \pi G \int_V \rho dV$$ just like in example 1 (above).

In other words, the integral of the gravity across the entire enclosing surface is proportional to the mass enclosed by the surface, regardless of the value of $r$. This is Gauss's law. It turns out to be applicable regardless of the mass distribution within the enclosing surface, or the shape of the enclosing surface. Because we know $G$ very well, the total mass can be determined by measuring the gravity field, without knowing anything about the mass distribution. From satellites (e.g., GRACE) we can measure gravity everywhere on a surface and so determine the mass of the Earth, despite the fact that mass is heterogeneously distributed in Earth. In fact, after Cavendish estimated $G$, a big activity of geophysicists was measuring $g$ around the globe to improve estimates of the Earth's mass.

[Top]

Example 3 of Gauss's law

What is the gravity field inside a planet?

Referring to the figure, if $R_E$ is the radius of the planet, what is the gravity at $r$, where: $$r < R_E$$ If the density of the planet is homogeneous, or only varies with the radius, $R_E$, then the mass of the spherical shell (between $r$ and $R_E$) has no gravitational force on the surface at $r$, so we only have to consider the mass of the planet inside $r$.

Assuming the planet is of a homogeneous density, $\rho$, the the total mass of the planet inside $r$ is \begin{align} M_E & = \frac{4}{3} \pi \rho R_E^3 \text{, } m = \frac{4}{3} \pi \rho r^3\\ \\ \textrm {therefore,}\\ \\ m & = M \frac{r^3}{R_E^3} \end{align} Given Gauss's law, \begin{align} \oint_S \vec g \cdot \vec n dA & = -4 \pi GM \\ -4 \pi r^2 g & = 4 \pi G M \frac{r^3}{R_E^3} \\ g & = G \frac{M}{R_E^3} r \end{align} gravity varies linearly with $r$ and $g \rightarrow 0$ as $r \rightarrow 0$.

The same approach works for finding gravity outside a planet ($r > R_E$). $$ \oint_S \vec g \cdot \vec n dA = -4 \pi GM $$ $$ -4 \pi r^2 g = 4 \pi G M $$ $$ g = G \frac{M}{r^2} $$ Outside the planet, gravity varies with $1/r^2$, and $g \rightarrow 0$ as $r \rightarrow \infty$. $g$ is maximum at $R_E$.