General least squares inversion - gravity of a buried sphere

Steps in solving the problem

To find the best-fit density:

• First, implement an analytical solution to calculate the gravity anomaly due to a buried sphere.
• Second, decide on the linear equation that can describe the observed variation in gravity. This will determine the basis functions for the problem, as described in the following.
• Implement a solution to the general least squares problem.
• Solve for the model gravity values.
• Visualize the results.
• Describe the error in the model.

General least-squares problem

Four things are needed for the generalized least squares problem:

• The observed data (e.g., $x_i, g_i$ where $i = 1...n$}, where $n$ is the number of gravity observations, each at horizontal position $x_i$ from the center of the sphere with observed gravity value $g_i$
• The general linear model (linear in $p_j$) where $j=1...m$ and $m$ is the number of unknown model parameters $$g_{model}(x) = p_1f_1(x) + p_2f_2(x) + ... + p_mf_m(x) = \sum_{j=1}^{m} p_j f_j(x)$$
• The $m$ chosen basis functions (a set of linear equations), that describe how the model parameters are thought to relate mathematically to the observations: $f_j(x)$ for $j = 1 ... m$
• The least-squares misfit criterion (what is the error between the model and the observations that we wish to minimize?) $$E = \sum_{i=1}^{n} e_i^2 = \sum_{i=1}^{n}(g_{model,i}(x_i) - g_{obs,i}(x_i))^2$$

Minimizing the misfit with respect to the unknown model parameters ($p_j$) means we must solve the $m$ linear equations that result from setting: $$\frac{\partial E}{\partial p_j} = 0 \text{ for all } j = 1 ...m$$ The gravity observations are arranged in a column vector: $$\mathbf b = \begin{bmatrix} g_{1} & g_{2} & g_{3} & \dots & g_{n} \end{bmatrix}^T $$ where $T$ indicates the transpose of the matrix

The matrix of basis functions is: $$\mathbf A = \begin{bmatrix} f_{11} & f_{12} & f_{13} & \dots & f_{1m} \\ f_{21} & f_{22} & f_{23} & \dots & f_{2m} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ f_{n1} & f_{n2} & f_{n3} & \dots & f_{nm} \end{bmatrix} $$ The matrix of unknown model parameters is: $$\mathbf x = \begin{bmatrix} p_1 \\ p_2\\ \vdots \\ p_m \end{bmatrix} $$ So, the predicted solution is: $$\mathbf g_{model} = \mathbf A \mathbf x$$ Knowing $\mathbf A$ and $\mathbf b$, we need to find the best $\mathbf x$, minimizing the difference between $\mathbf g_{model}$ and $\mathbf b$.

The general least-square solution is: $$\mathbf x = (\mathbf A^T \mathbf A)^{-1} \mathbf A^T \mathbf b $$

Linear equation to describe the gravity anomaly due to a buried sphere

One solution to the problem is to implement basis functions in the form: $$ g_{model}(x) = p_1 + p_2 x + p_3 x^2 + p_4 g_{sphere}(z,r,x)$$ where $p_1, p_2, p_3$ are coefficients that attempt to account for the regional variation in gravity using a quadratic equation. The function $g_{sphere}(z,r,x)$ is just like the function implemented to calculate the gravity anomaly due to a sphere, with the important exception that the function returns the estimated gravity anomaly divided by the density. In this case the parameter $p_4$ is the estimated density contrast. This model assumes that the depth of the sphere, its horizontal location, and its radius are known.

An implementation of this solution, assuming the sphere is located at zero offset, is: $$\begin{bmatrix} 1 & x_1 & x_1^2 & g_{sphere}(z,r,x_1) \\ 1 & x_2 & x_2^2 & g_{sphere}(z,r,x_2) \\ \vdots & \vdots & \vdots & \vdots \\ 1 & x_n & x_n^2 & g_{sphere}(z,r,x_n) \end{bmatrix} \begin{bmatrix} p_1 \\ p_2 \\ p_3 \\ p_4 \end{bmatrix} = \begin{bmatrix} g_1 \\ g_2 \\ \vdots \\ g_n \end{bmatrix} $$ In words, the set of linear equations (the basis functions) are related to the observed gravity by a vector of four unknown parameters. The problem is solved for the vector of four unknown parameters using the general least-square solution provided above.

perl code to invert the gravity anomaly due to a buried sphere

This code requires an additional library, Math::MatrixReal. Install this package with the command line perl installation program, cpan.

#!/usr/bin/perl

# estimate the density contrast from gravity 
# data assuming a buried sphere beneath a horizontal surface
# with regional gradient in gravity modeled
# with a third order polynomial.
# This code demonstrates the use of general least-square 
# solution for the inversion of gravity data

# C. B. Connor
# last modified October, 2015

use warnings;
use strict;
use Math::MatrixReal;

#######################################################
#subroutine to calculate the gravity anomaly due to a buried sphere

# inputs:
#     1) sphere radius (m) 
#     2) sphere depth (m) 
#     3) horizontal distance of station
#        location (calculation point) from 
#        center of sphere (m)
#
# output:
#     gravity anomaly value divided by the density contrast

# multiply the result by the density contrast (kg/m3) 
# to get the gravity anomaly (mGal)
###########################################################
sub gsphere ($$$) {

  my $pi = 3.14159265358979;
  my $a = shift; #input the radius of the sphere (m)
  my $z = shift; #input the depth of the center of the  
               # sphere (m)
  my $x = shift; #input the horizontal distance of the 
               #location of the gravity observation (m)

  my $big_G = 6.67e-11;
  my $to_mgal = 1e5;

  my $V = (4/3)* $pi * $a ** 3;
  my $grav = $to_mgal * $big_G * $V * $z * (($z*$z + $x * $x) ** (-3/2));

  return $grav;
}

####################################
# MAIN routine starts here:
# Construct an example data set of gravity observations to test the inversion
# normally this section will be replaced with actual data
# in the arrays @x and @obs_gravity
####################################
my $n = 0; #number of gravity observations
my $i = 0; #counter
my $c1, my $c2, my $c3, my $c4; #unknown model parameters
my @x; #horizontal offset
my @obs_gravity; # observed gravity data
my @model_gravity; #model gravity data
my $grav_data; #observed gravity data in array for GLS solution

# The center of the sphere is assumed to be located at 0 m. 
# Assigned some properties to the sphere.
my $sphere_radius = 4000; #m
my $sphere_depth = 5000; #m (sphere_depth > sphere_radius)
my $sphere_density_contrast = 500; #kg/m3

# Assign some values to the polynomial coefficients
# to produce a regional gradient in the 
# "observed" gravity data.
$c1 = 0.0;
$c2 = 0.001;
$c3 = 0.000000005;

# Calculate the "observed" gravity anomaly
# at a series of locations @x 
for ($i = 0; $i <= 50; $i++) {
	# horizontal distance (m from sphere center)
  $x[$i] = ($i-25) * 1000; 
  # tally the number of gravity readings          
  $n++;                   
  $obs_gravity[$i] = $c1 + $c2*$x[$i] + $c3*$x[$i]**2 + $sphere_density_contrast * gsphere($sphere_radius, $sphere_depth, $x[$i]);
  # Add some uncertainty to the observations
  $obs_gravity[$i] += rand(4.0)-2.0; 
}
  
# The general least-squares model:
# Build the basis functions (A matrix)
# and assign the gravity observations to an appropriate mtx
my $A = new Math::MatrixReal($n,4);
$grav_data = new Math::MatrixReal($n,1);

for ($i = 1; $i < $n; $i++) {
     $A->assign($i, 1,1);
     $A->assign($i, 2,$x[$i]);  
     $A->assign($i, 3, $x[$i]*$x[$i]); 
     $A->assign($i, 4, gsphere($sphere_radius, $sphere_depth, $x[$i])); 
     $grav_data->assign($i, 1, $obs_gravity[$i]);
}

# Solve for the unknown model parameters
my $AT = $A->new(4,$n);
$AT->transpose($A);
my $AAT = $AT * $A;
my $inv_AAT = $AAT->inverse;
my $AAAT = $inv_AAT * $AT;
my $p = $AAAT*$grav_data;

# Assign each model parameter to its own varible
$c1 = $p->element(1,1);
$c2 = $p->element(2,1);
$c3 = $p->element(3,1);
$c4 = $p->element(4,1);

print "# ";
print "p1 = $c1, p2 = $c2, p3 = $c3, p4 = $c4\\n";

# Run the forward model with the estimated parameters
# Print out model, to compare the model and observed data
for ($i= 0; $i<=50; $i++) {
   $model_gravity[$i] = $c1 + $c2*$x[$i] + $c3*$x[$i]**2 + $c4*gsphere($sphere_radius, $sphere_depth, $x[$i]);
   print "$x[$i] $model_gravity[$i] $obs_gravity[$i]\n";
};

In this example, the observed gravity data are generated in order to test the code. Specifically, a forward solution is calculated using a set of model parameters. Afterwards, random variation is added to the data using the perl function rand(). Normally, the section that creates the observed data will be replaced by an function that reads an input file of gravity station location and observed gravity values.

The following table compares the generated input parameters with the calculated output parameter estimates, for one run. Note that the output will vary each time the code is run because the rand() function introduces a different randomness each time the code is run.

Plotting the output with gnuplot

Two plots of the output from the perl script show a comparison of the model (calculated) gravity data with the observed (generated) gravity data. Plot A shows a profile of the grvity anomaly. Plot B is an equaline plot. If the inversion was perfect, all of the points would fall on the black line. These simple plots were generated using gnuplot.

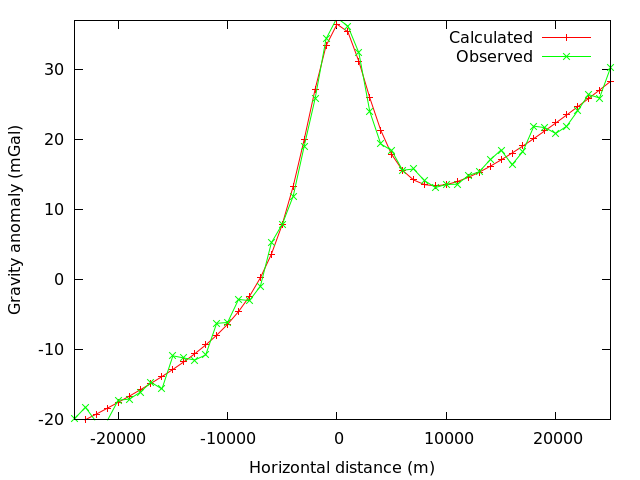
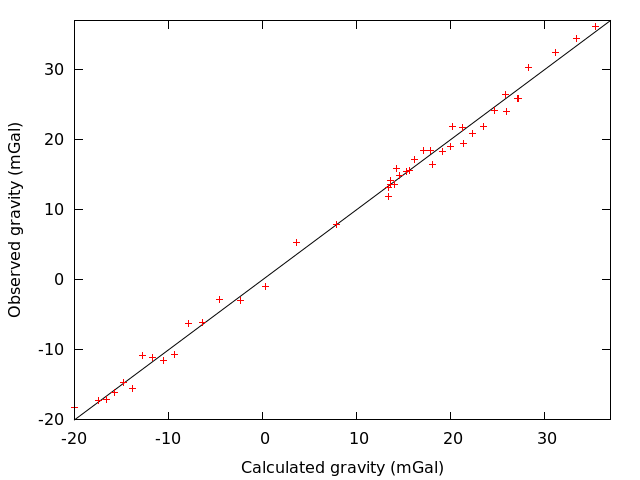
# USAGE 
# type: gnuplot plot_grav.gnu
# on the command line
reset

set terminal pngcairo
set output "sphere_inversion1.png"

# Axes label
set xlabel 'Horizontal distance (m)'
set ylabel 'Gravity anomaly (mGal)'

# Axes ranges
set xrange [-24000:25000]
set yrange [-20:37]

# Axes tics
set xtics 10000
set ytics 10

plot  "sphere_inversion.dat" using 1:2 with linespoints title 'Calculated', \
      "sphere_inversion.dat" using 1:3 with linespoints title 'Observed'

# USAGE:
# type: gnuplot equaline_plot.gnu
# on the command line
reset
set terminal pngcairo
set output "sphere_inversion2.png"

# Axes label
set xlabel 'Calculated gravity (mGal)'
set ylabel 'Observed gravity (mGal)'

# Axes ranges
set xrange [-20:37]
set yrange [-20:37]

# Axes tics
set xtics 10
set ytics 10

set arrow from -20,-20 to 37,37 lc rgb "black" nohead
plot  "sphere_inversion.dat" using 2:3 title ''

Parameter error

If the data error are normally distributed with variance $\sigma^2$ (e.g., measurement error), it is possible to estimate the parameter error directly:

The number 1.96 indicates that the confidence interval on the parameter estimate is 95 percent. For example, the following lines of code might be added to the script to include an estimate of the uncertainty in parameters due to measurement error:

#error on parameters
   my $variance = 1.0; #square mGal
   my $C = $variance*$inv_AAT;
   my $c1_error = 1.96 * $variance * sqrt($C->element(1,1));
   my $c2_error = 1.96 * $variance * sqrt($C->element(2,2));
   my $c3_error = 1.96 * $variance * sqrt($C->element(3,3));
   my $c4_error = 1.96 * $variance * sqrt($C->element(4,4));
print "p1 = $c1 +/- $c1_error, p2 = $c2+/- $c2_error, p3 = $c3+/- $c3_error, p4 = $c4+/- $c4_error\n";

This error estimate assumes that the model is correct. That is, that the quadratic equation plus the sphere forward model actually is the correct model. An example of the error estimates on model parameters, using a variance of 1 mGal:

Assuming the gravity anomaly can be modeled by a buried sphere, the density contrast in this case is estimated to be in the interval 494 to 530 kg m$^{-3}$ with 95 percent confidence.

Some References

1. Telford, W.M., Geldart, L.P. and Sheriff, R.E. (1990) Applied Geophysics, Cambridge University Press.
2. MacMillan, W.D. (1958) The Theory of the Potential, Dover Books on Science and Engineering, New York.