Gravity anomaly due to a thin vertical rod
Calculate the gravity anomaly due to a thin vertical rod
Introduction
Find the gravity anomaly due to a thin vertical rod. The rod is
[Top]
the vertical component of the gravity anomaly, $g_z$, can be calculated by,
\begin{align}
g_z & = G A \Delta \rho \int_{0}^{L} \frac{(z + l)dl}{\left [x^2 + (z+l)^2 \right ]^{1/2} (x^2 + (z+l)^2)}\\
u & = (z+l)^2\\
du & = 2(z+l) dl\\
g_z & = G A \Delta \rho \int \frac{du}{\left [x^2 + u \right ]^{3/2}}\\
g_z & = -G A \Delta \rho \left [x^2 + (z+l)^2 \right ]^{-1/2} |_0^L\\
g_z & = G A \Delta \rho \left [\frac{1}{\sqrt{x^2+z^2}} - \frac{1}{\sqrt{x^2 + (z+L)^2}} \right ]
\end{align}
Mathematical model
The gravity anomaly due to a thin vertical rod can be calculated using the following equation, $$g_z = G A \Delta \rho \int_0^L \frac{dl}{r^2} \cos \theta$$ where,
- $A$ is the cross sectional area of the rod
- $G$ is the gravitational constant
- $\Delta \rho$ is the density contrast between the rod and the surrounding medium (surrounding rock)
- $L$ is the length of the rod
- $r$ is the distance from the measurement point to the center of segment $dl$
- $\theta$ is the angle of $r$ wrt vertical.
Based on the geometry illustrated in this figure,
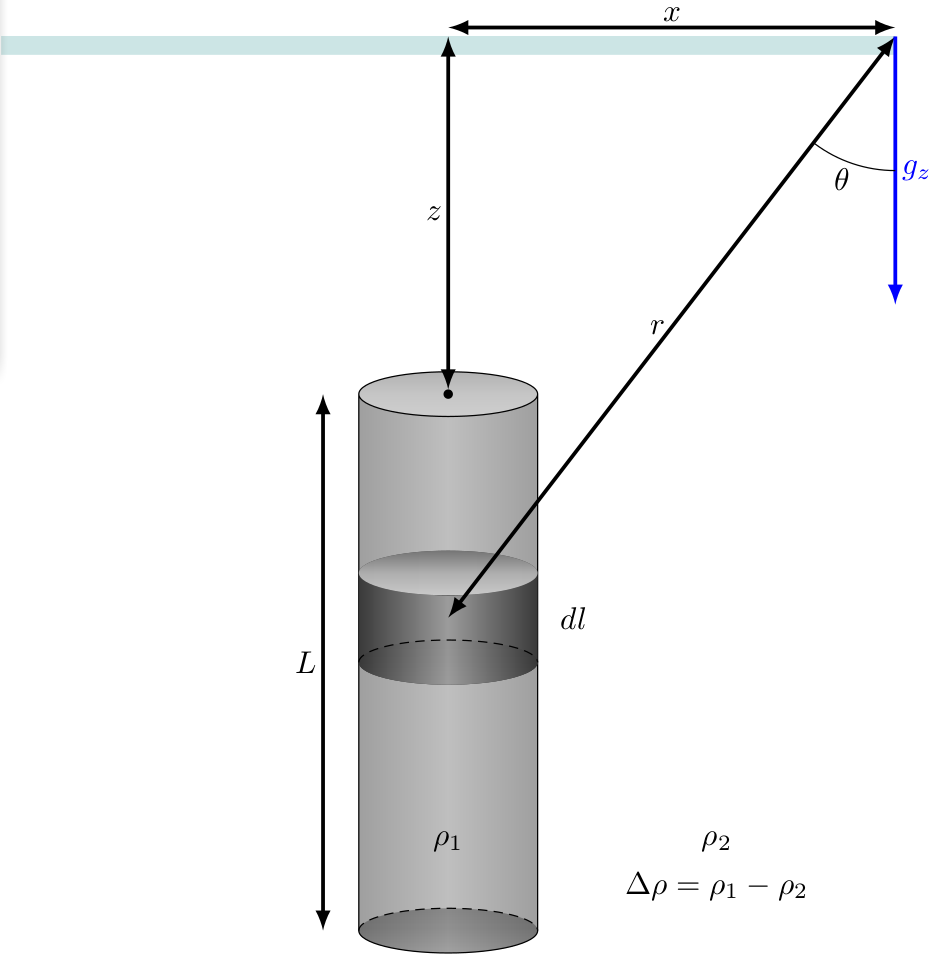
As the length of the rod becomes very long, the expression reduces to, $$g_z = \frac{GA \Delta \rho}{\left [ \sqrt{x^2 + z^2}\right ]}.$$
[Top]
LaTeX script: vert_rod.tex
Drawing with LaTeX and TikZ
The following LaTeX and TikZ code draws the figure of the model geometry presented at the top of the page.
\documentclass{article}
\usepackage{tikz}
\usetikzlibrary{calc,fadings,decorations.pathreplacing}
\usetikzlibrary{shadings}
\usepackage{verbatim}
\usepackage{verbatim}
\usepackage[active,tightpage]{preview}
\PreviewEnvironment{tikzpicture}
\setlength\PreviewBorder{5pt}%
\tikzset{%
>=latex, % option for nice arrows
inner sep=0pt,%
outer sep=2pt,%
mark coordinate/.style={inner sep=0pt,outer sep=0pt,minimum size=3pt,
fill=black,circle}%
}
\begin{document}
\begin{tikzpicture}
%big cylinder
\fill[top color=gray!50!black,bottom color=gray!10,middle color=gray,shading=axis,opacity=0.25] (0,0) circle (1cm and 0.25cm);
\fill[left color=gray!50!black,right color=gray!50!black,middle color=gray!50,shading=axis,opacity=0.25] (1,0) -- (1,6) arc (360:180:1cm and 0.25cm) -- (-1,0) arc (180:360:1cm and 0.25cm);
\fill[top color=gray!90!,bottom color=gray!2,middle color=gray!30,shading=axis,opacity=0.25] (0,6) circle (1cm and 0.25cm);
\draw (-1,6) -- (-1,0) arc (180:360:1cm and 0.25cm) -- (1,6) ++ (-1,0) circle (1cm and 0.25cm);
\draw[densely dashed] (-1,0) arc (180:0:1cm and 0.25cm);
%cylinder segment
\fill[top color=gray!50!black,bottom color=gray!10,middle color=gray,shading=axis,opacity=0.75] (0,3) circle (1cm and 0.25cm);
\fill[left color=gray!50!black,right color=gray!50!black,middle color=gray!50,shading=axis,opacity=0.75] (1,3) -- (1,4) arc (360:180:1cm and 0.25cm) -- (-1,3) arc (180:360:1cm and 0.25cm);
\fill[top color=gray!90!,bottom color=gray!2,middle color=gray!30,shading=axis,opacity=0.75] (0,4) circle (1cm and 0.25cm);
%\draw (-2,4) -- (-2,3) arc (180:360:2cm and 0.5cm) -- (2,4) ++ (-2,3) circle (2cm and 0.5cm);
\draw[densely dashed] (-1,3) arc (180:0:1cm and 0.25cm);
\draw[teal, line width = 6, opacity = 0.2] (-5,9.9) -- (5,9.9) ;
\coordinate [mark coordinate](O) at (0,6);
\draw[<->, very thick] (O) -- node[left]{$z$} (0,10) ;
\draw[<->, very thick] (0,3.5) -- node[left]{$r$} (5,10) ;
\draw[<->, very thick] (0,10.1) -- node[above]{$x$} (5,10.1) ;
\draw[<->, very thick] (-1.4,0) -- node[left]{$L$} (-1.4, 6) ;
\node at (1.4,3.5) {$dl$};
\draw[blue, very thick, ->] (5,10) -- node[right]{$g_z$} (5,7);
\draw [black] (5,8.5) arc [radius=1.5, start angle=-90, end angle= -127];
\node at (4.4,8.4) {$\theta$};
\node at (3,1) {$\rho_2$};
\node at (0,1) {$\rho_1$};
\node at (3,0.5) {$\Delta \rho = \rho_1 - \rho_2$};
\end{tikzpicture}
\end{document}