Inverting tephra fallout deposit data
Learn about modifying Tephra2 to determine eruption mass and an eruption column parameter for the 1992 Cerro Negro (Nicaragua) eruption using simulated annealing
Introduction
Now we modify the inversion code to include two parameters that are estimated simultaneously: total eruption mass and "alpha". Many tephra scientists seek to estimate total eruption mass (or volume) and estimate eruption column propoerties, especially the maximum eruption column height. Instead of estimating the eruption column height, we are going to estimate alpha, which is a parameter that controls the distribution of tephra within the eruption column. Alpha is a parameter in an equation called the Beta distribution (confusing enough!), the Beta distribution has two parameters, $\alpha$ and $\beta$. By fixing $\beta$ we can vary $\alpha$ to have more or less tephra distributed from high in the eruption column compared to from lower in the eruption column. The effect of changing $\alpha$ with fixed values of $\beta$ is shown in this figure:
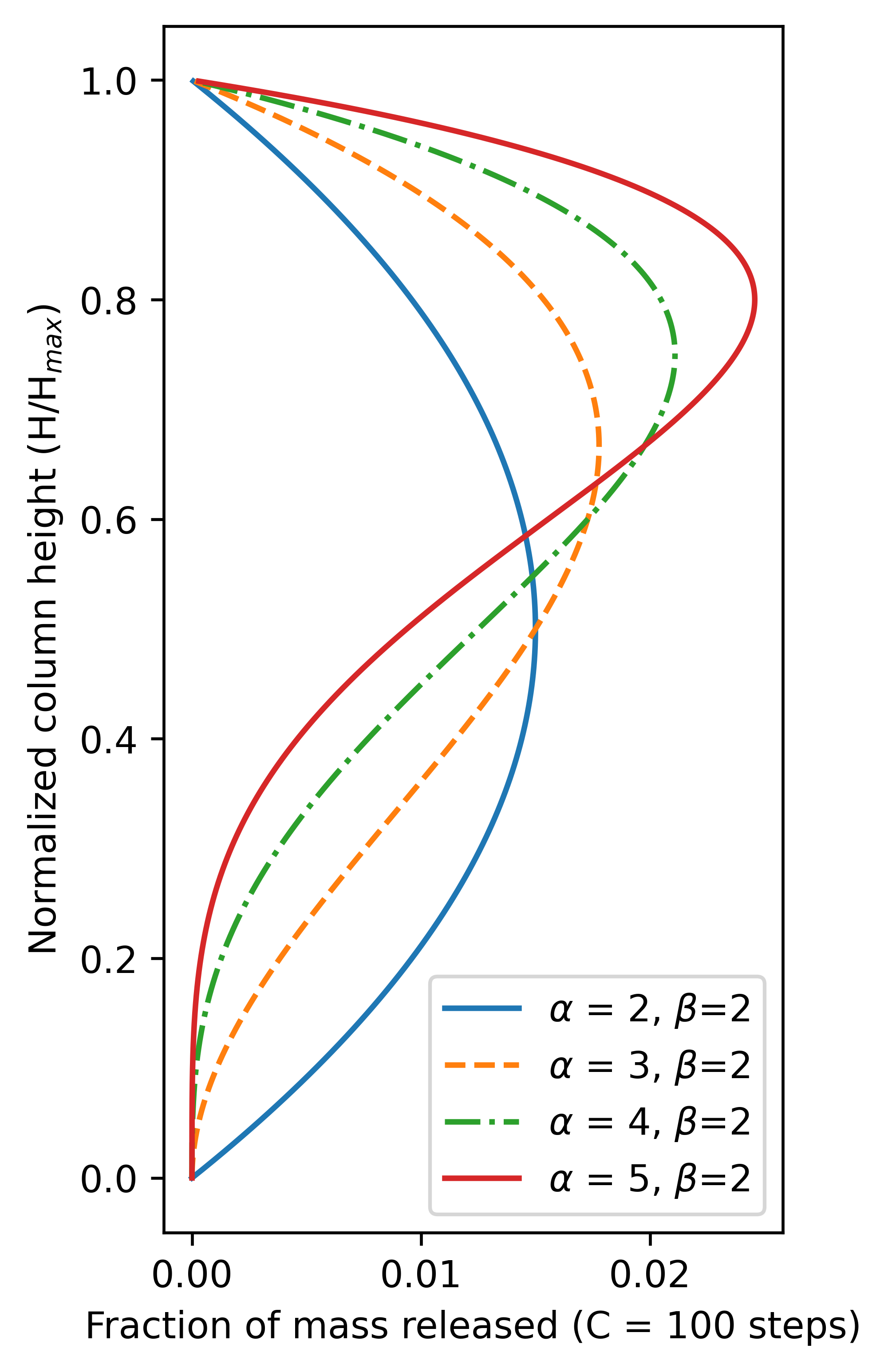
Whatever the eruption column height, a large value of $\alpha$ compared to $\beta$ will tend to release most tephra toward the top of the eruptin column (like a so-called top-hat model of the eruption plume). In contrast if $\alpha$ is nearly equal to $\beta$, most tephra will be released in the mid-column. This might be appropriate for an eruption column that reaches its maximum height briefly, but spends most of its time with shorter, or pulsing, columns.
Structure of the Inversion
The basic structure of this inversion is illustrated in the flowchart. Two bits of information are needed:
- The input data file consists of the x,y, and elevation coordinates of the tephra mass loading observations, the mass loading value value, and, initially, a column of zeros, representing the calculated mass loading.
- The initial eruption source parameters. All parameters are set in this input, which is a configuration file. Only one parameter (total eruption mass in this case) will be adjusted. Note that the tephra configuration file is input from the command line when the code is executed.
With these inputs the main() code calls the function to perform the search for the optimal eruption total mass and alpha simulated annealing (SA) algorithm. Using SA, the parameters are updated, the new expected tephra mass loading at each location is calculated and root-mean-square-error is calculated comparing the observed and calculated tephra mass loading values.
Just like before, the RMSE is minimized within some tolerance, the optimal total eruption mass and RMSE value are printed.
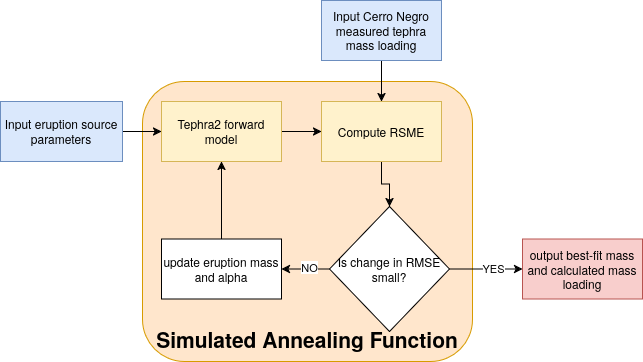
Other eruption soure parameters specified in the configuration file are fixed in this example. Only two parameters, the total eruption volume and the value of alpha are allowed to vary in the inversion procedure.
The Simulated Annealing Search to Estimate Two Parameters
This function, simulated_annealing, is an implementation of the Simulated Annealing (SA) optimization algorithm for finding the optimal total eruption mass and alpha parameters that minimizes the root mean square error (RMSE) between observed and calculated tephra mass loadings.
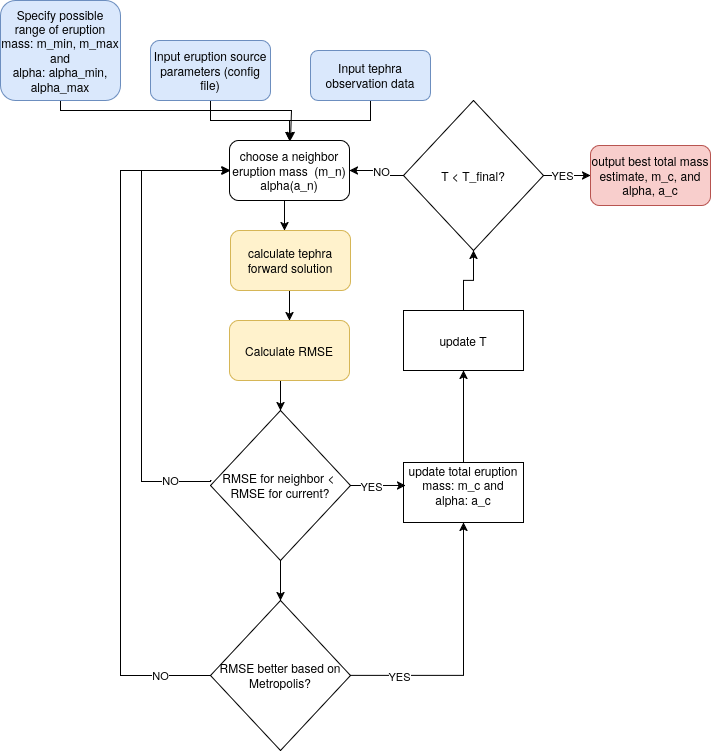
The key steps are the same as before, just with an additional parameter to be estimated:
- Initialize the Bounds: Set an initial range for possible eruption mass: $m_{min} = 1 \times 10^{10}$ kg m$^{-2}$ and $m_{max} = 1 \times 10^{11}$ kg m$^{-2}$ . Alpha is going to vary between 2 and 5, with "beta" fixed to 2 in the configuration file. Choose a "current total eruption mass" and "current alpha" within these bounds. These choices might be arbitary or might be based on what the solution is expected to be.
- Specify the initial and final temperature of the calculation, the cooling rate, and the maximum number of iterations allowed. These parameters control the search for the best-fit total eruption mass and alpha values.
- Iterative Optimization:
- Step 1: Choose a neighboring total eruption mass parameter, adjacent to the "current total eruption mass". The neighbor eruption mass is: $$m_n = m_c + \left [ \frac{\textrm{rand()}}{\textrm{RAND_MAX}} - 0.5\right ] \times (m_{max} - m_{min}) \times 0.1$$ The neighbor alpha is found in exactly the same way: $$a_n = a_c + \left [ \frac{\textrm{rand()}}{\textrm{RAND_MAX}} - 0.5\right ] \times (a_{max} - a_{min}) \times 0.1$$ These equations ensure that the neighbor parameters are within $\pm 5$ percent of the total parameter range. But a checks are made to make sure $m_{min} < m_n < m_{max}$ and $a_{min} < a_n < a_{max}$.
- Step 2: Compute the new tephra fallout mass loading at each obsrvation point with the $m_n$ and $a_n$ values and update the RSME
- Step 3: Both $m_n$ and $a_n$ become the current parameter values if either the new RSME is lower or the RMSE is worse based on the Metropolis criterion: $$\exp(-\Delta \textrm{RSME}/T) > \frac{\textrm{rand()}}{\textrm{RAND_MAX}} $$ which means that nearby worse depth estimates are accepted (temporarily) with some probability that depends on the temperature ($T$). This approach helps the SA algorithm escape from local minima in the RMSE function (for example because the data are noisy).
- If the current total eruption mass $m_c$ and alpha are updated, then the temperature ($T$) is reduced by a factor of $\alpha_T$: $$T = \alpha_T T $$ Usually $\alpha_T = 0.9$ to gradually decrease the temperature. So, the value of $T$ changes throughout the search. Early on in the search, $T$ is large, so "bad" moves are accepted leading to exploration of the entire range of possible eruption mass and alpha values. As the search continues, $T$ becomes smaller and the search focuses only on better moves (lower RMSE values).
- Return the Optimal total eruption mass and optimal alpha when the $T_{final}$ value is reached.
The C code
You need a bunch of files to compile and run this code. These files are contained in a compressed file called tephra2-inversion2-victor.zip.
Download this compressed file and unzip. To compile the code, on the command line type: make
To run the code type: ./tephra2_2025 tephra2.conf cerro_negro_92.dat wind1 > cn_out.dat
If all goes well, the first lines of your output file should look like:
Optimized mass: 30718717835.014091
Optimized alpha: 4.096587
Best RMSE: 232.923827
526774 1381087 100 509.00 554.681
526028 1380972 100 256.00 435.878
525477 1380291 100 476.00 317.361
524516 1379866 100 249.00 229.531
523595 1379462 100 244.94 173.98
522674 1379481 100 227.00 156.622
521642 1379304 100 171.60 130.694
In this case the RMSE is 233kg m$^{-2}$ for a total eruption mass of approximately $3.1 \times 10^{10}$ kg. Alpha has a best-fit value of about 4, indicating that most mass is release from relatively high in the eruption column, consistent with an energetic eruption (high mass flow). NOTE: when you run the code you will get a slightly different answer. This is because the simulated annealing algorithm uses a random number to select the neighbor parameter values. In fact, running the code over and over with the same parameters provides some sense of the parameter uncertainty.
As before, it is helpful to plot an equiline plot of the observed vs. calculated mass at each sample location, based on the estimate of the optimal total eruption mass and alpha. For this solution, the equiline plot looks like:
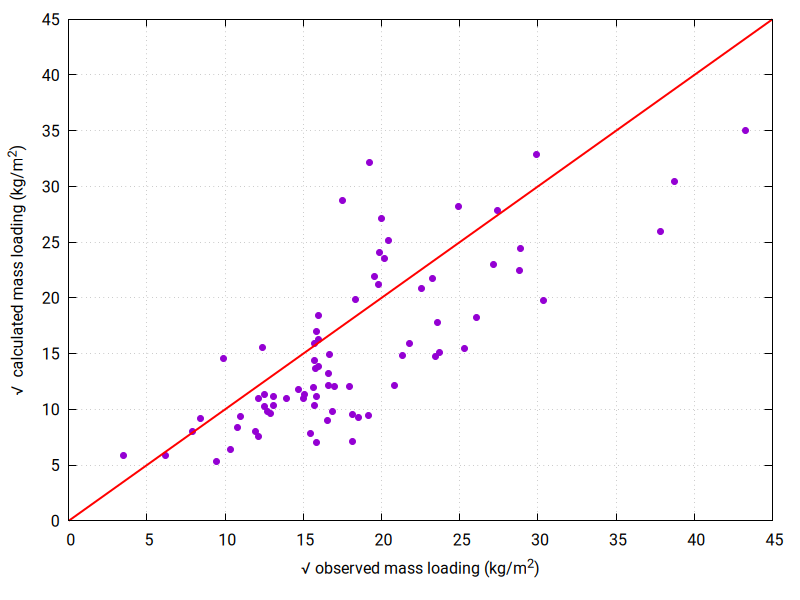
Note that based on RMSE, the solution for the previous example (only inverting on total eruption mass) and this one (inverting on total eruption mass and alpha) are similar, although the total eruption masses estimated are different. It looks like a range of total eruption masses fit the data equally well. That is, there is uncertainty in the value of this eruption source parameter.
Things to Try
- Make sure you can download, compile and run the code. Plot up the output to compare the observed and calculated tephra fallout deposits.
- Try modifying the inversion by changing the eruption source parameters in the configuration file. How does the estimated eruption mass and alpha change? In particular, try entering a very high eruption column (like 12500 m) and see what happens to the best estimate of alpha. Does this answer make sense? This is an example of parameter compensation. If you change the range of one parameter, another parameter value can change to compensate and result is a similar goodness-of-fit.
- In the current version of the code, the maximum and minimum total eruption mass parameters are specified in main(). Try modifying the code so these parameters are read from a configuration file. Hint: see the C shortcourse for an example of reading a configuration file: data4.c