Inverting tephra fallout deposit data

Learn about modifying Tephra2 to estimate many eruption source parameters for the 1992 Cerro Negro (Nicaragua) eruption using simulated annealing

Contents

Introduction

Now we modify the inversion code to include four parameters that are estimated simultaneously: total eruption mass, maximum eruption column height, "alpha", and median grainsize of the deposit. This analysis still uses simulated annealing, but is now a multi-parameter estimation problem. In addition, this analysis pays more attention to parameter uncertainty. This is achieved by running the inversion many times, say 100 times, and finding the range of parameters that result in solutions with reasonable small root-mean-square-error (RMSE).

[Top]

The Simulated Annealing Search to Estimate Four Parameters

The same overall code structure is maintained in this example. Primarily, the simulated annealing function is modified to include search for four parameters: total eruption mass, maximum eruption column height, "alpha", and median grainsize of the deposit. Any one inversion produces a set of these four parameters and an RMSE value. Because simulated annealing uses a random number generator to select neighbor solutions, the best-fit parameters will change each time the code is executed. So, by running the inversion many times, the uncertainty in the eruption source parameters can be estimated.

In this example, the inversion is executed 100 times in order to get a sense of parameter uncertainty. For each simulation, the "optimal" parameter set is printed to output. Since the SA algorithm uses a random seed to start the simulation, each time a different solution is identified and printed. The flow chart for this procedure is:

sim flowchart

The key steps are the same as before, just with an additional parameter to be estimated:

  • Initialize the Bounds. Note the bounds on all parameters are now set in a data structure in main ())
  • Specify the initial and final temperature of the calculation, the cooling rate, and the maximum number of iterations allowed. These parameters control the search for the best-fit total eruption mass and alpha values.
  • Iterative Optimization:
    • Step 1: Choose a neighboring total eruption mass parameter, adjacent to the "current total eruption mass". The neighbor eruption mass is: $$m_n = m_c + \left [ \frac{\textrm{rand()}}{\textrm{RAND_MAX}} - 0.5\right ] \times (m_{max} - m_{min}) \times 0.1$$ The neighbor alpha, column height and median grainsize are found in exactly the same way:
    • Step 2: Compute the new tephra fallout mass loading at each observation point with the neighbor parameter values and update the RSME
    • Step 3: Neighbor parameter values become the current parameter values if either the new RSME is lower or the RMSE is worse based on the Metropolis criterion: $$\exp(-\Delta \textrm{RSME}/T) > \frac{\textrm{rand()}}{\textrm{RAND_MAX}} $$ which means that nearby worse depth estimates are accepted (temporarily) with some probability that depends on the temperature ($T$). This approach helps the SA algorithm escape from local minima in the RMSE function (for example because the data are noisy).
    • If the current parameter values are updated, then the temperature ($T$) is reduced by a factor of $\alpha_T$: $$T = \alpha_T T $$ Usually $\alpha_T = 0.9$ to gradually decrease the temperature. So, the value of $T$ changes throughout the search. Early on in the search, $T$ is large, so "bad" moves are accepted leading to exploration of the entire range of possible eruption mass and alpha values. As the search continues, $T$ becomes smaller and the search focuses only on better moves (lower RMSE values).
    • Return the Optimal total eruption mass and optimal alpha when the $T_{final}$ value is reached.

[Top]

The C code

You need a bunch of files to compile and run this code. These files are contained in a compressed file called tephra2-inversion3-victor.zip.

Download this compressed file and unzip. To compile the code, on the command line type: make

To run the code type: ./tephra2_2025 tephra2.conf cerro_negro_92.dat wind1 > cn_out.dat

If all goes well, the first lines of your output file should look like:


# eruption_mass, alpha, median phi, max plume height, rmse
30021943727.285576 3.180860 -0.056335 7155.299129 252.018181
41108341352.133232 3.395728 0.873463 7313.697391 218.149899
27261214988.893471 3.604860 -0.553366 8866.659696 240.702996
35450434898.701698 3.902670 0.603898 6110.914288 228.479505
29244515074.763687 3.168427 -0.032769 7527.717714 246.658578
34611805124.260399 3.723994 -0.074945 8240.863971 227.447151
39764786277.322464 4.091041 0.784999 7264.116956 216.192832
30071700615.608921 3.679748 0.037787 6703.240077 242.700108

Parameter sets are printed for each "optimal" solution along with the RMSE for that solution. Note that your solutions will not be exactly the same, since a random seed uis used in the code to start the SA search.

You can explore the output by plotting histograms of parameter values and by plotting scatter plots to search for correlation among estimated parameter values:

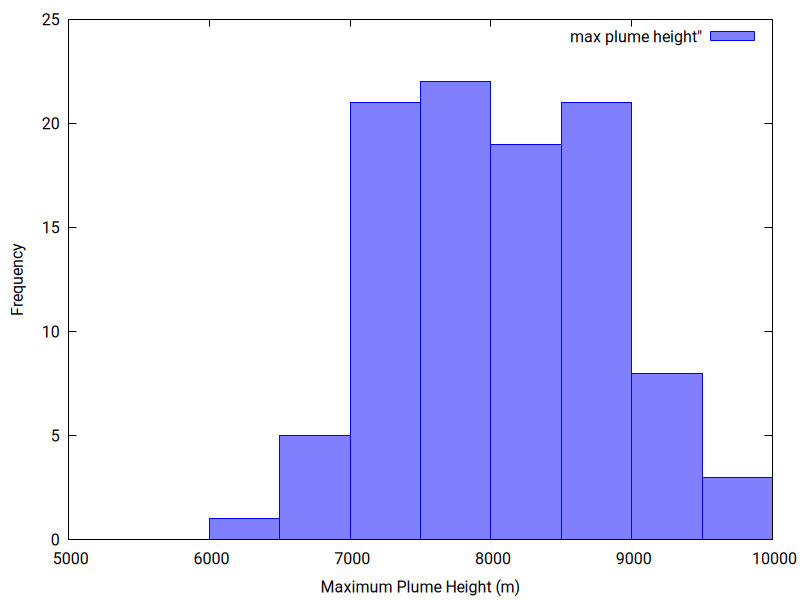
mass histogram max plume histogram
Eruption mass histogram (left) and maximum plume height histogram (right). The simulations yield reasonable ranges for total eruption mass and maximum eruption column height. Both parameter estimates show some central tendency.
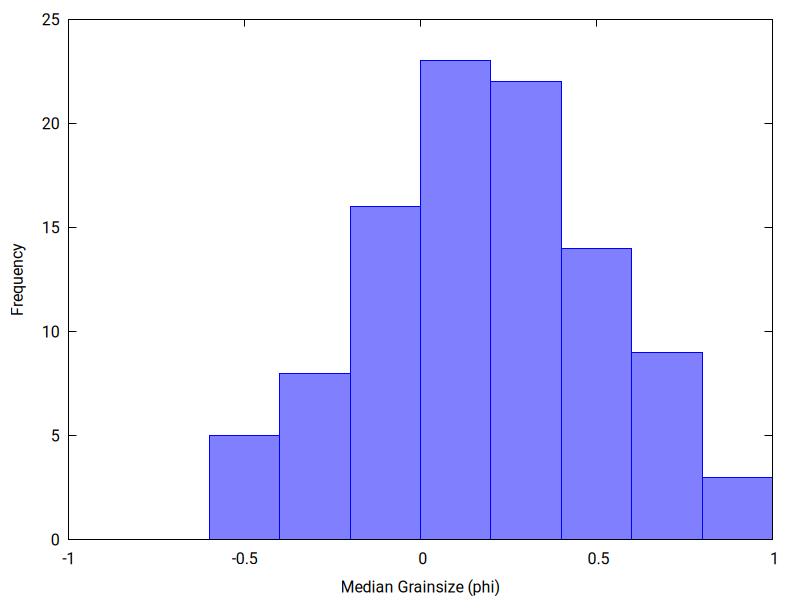
median phi histogram alpha histogram
Median of the total eruption grainsize distribution (left) and alpha (right). The simulations yield reasonable ranges for these ESPs. The median grainsize has central tendency to about +0.2 phi. Alpha has a best estimate of around 3.6, meaning most of the mass is concentrated relatively near the top of the eruption column.
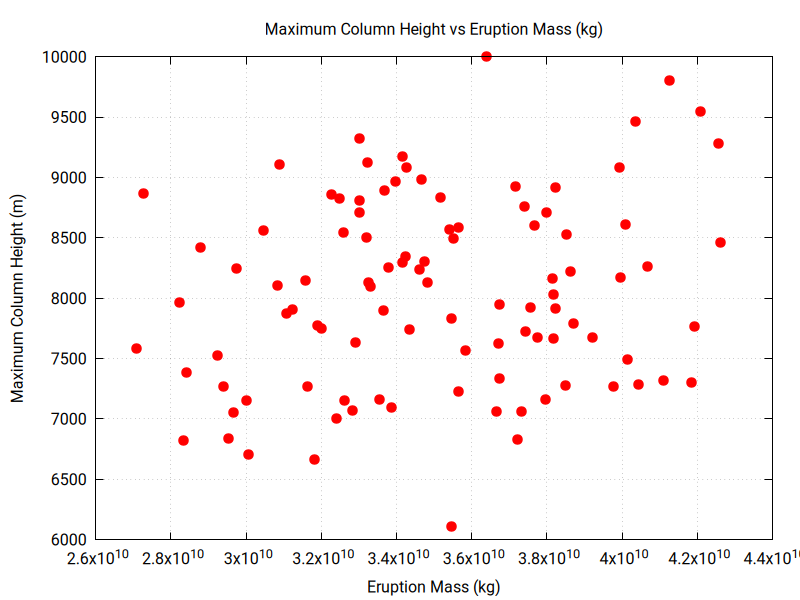
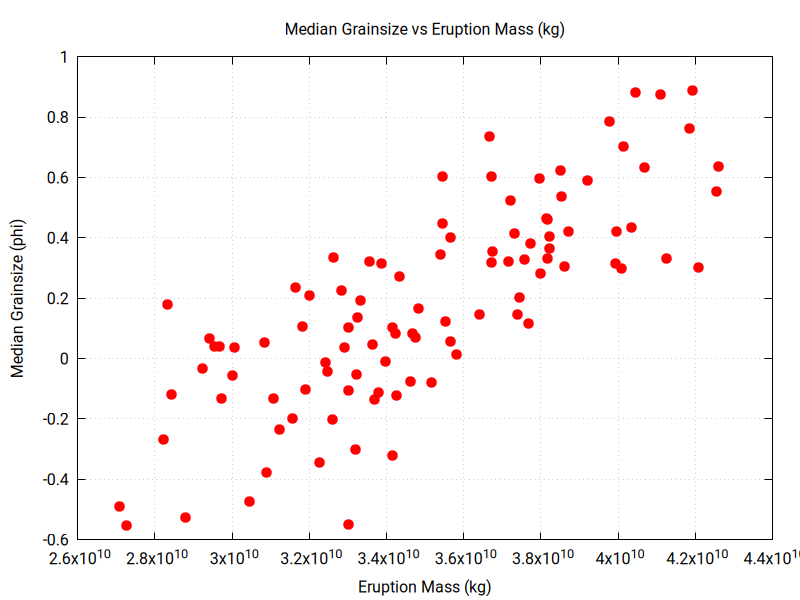
mass vs plume height mass vs. grainsize
It is also important to search for correlation among the estimated eruption source parameters. In this case, there is a very slight positive correlation between eruption mass and maximum plume height. There is a clear correlation between eruption mass and median grainsize. As the eruption mass becomes larger, median grainsize tends toward finer grainsize (larger positive phi values). Since finer grainsizes are more widely dispersed compared to coarser grainsizes (due to their slower settling velocities), the eruption mass can increase. In other words, more mass is deposited in distal locations by these simulations.
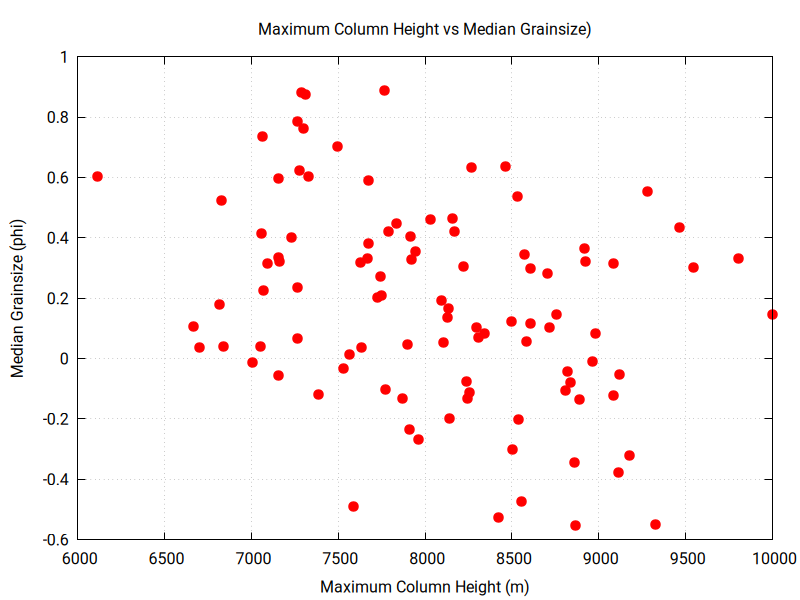
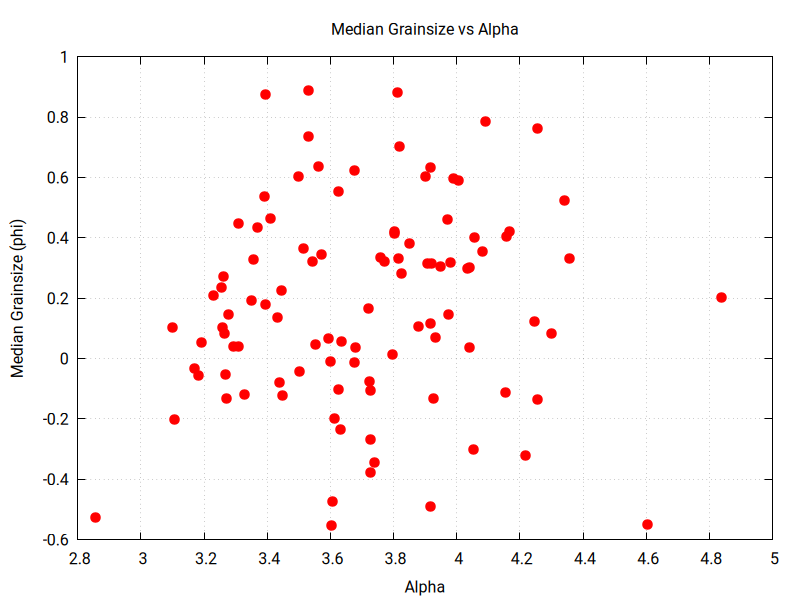
plume height vs grainsize alpha vs grainsize
Likewise, a slight negative correlation is observed between maximum eruption column height and median grainsize. As the eruption column height parameter increases, the best-fit median grainsize becomes coarser. This makes sense, as coarser particles fall at greater speed from higher in the column. There is no observed correlation between grainsize and alpha, the eruption column shape parameter.

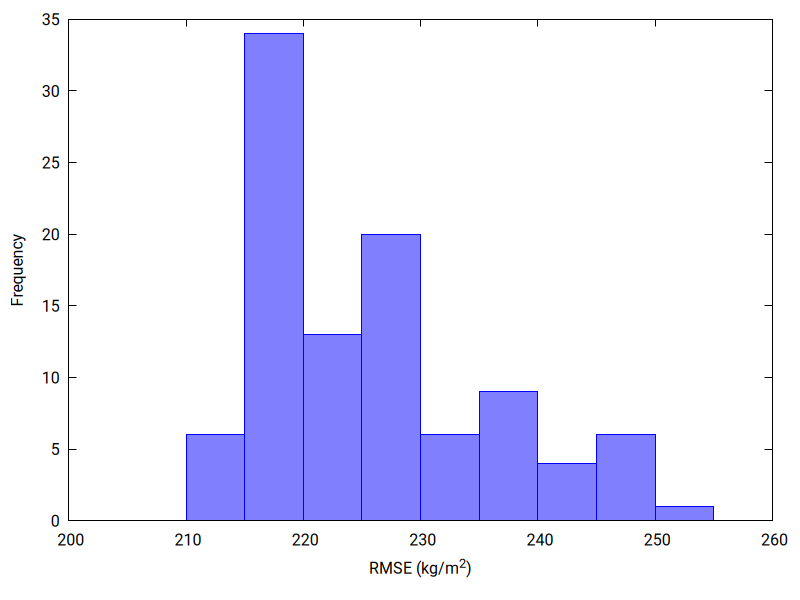
The 100 inversions have some variation in best-fit RMSE value:

sim flowchart

One solution is selected from this group of 100 solutions and the equiline plot is made:

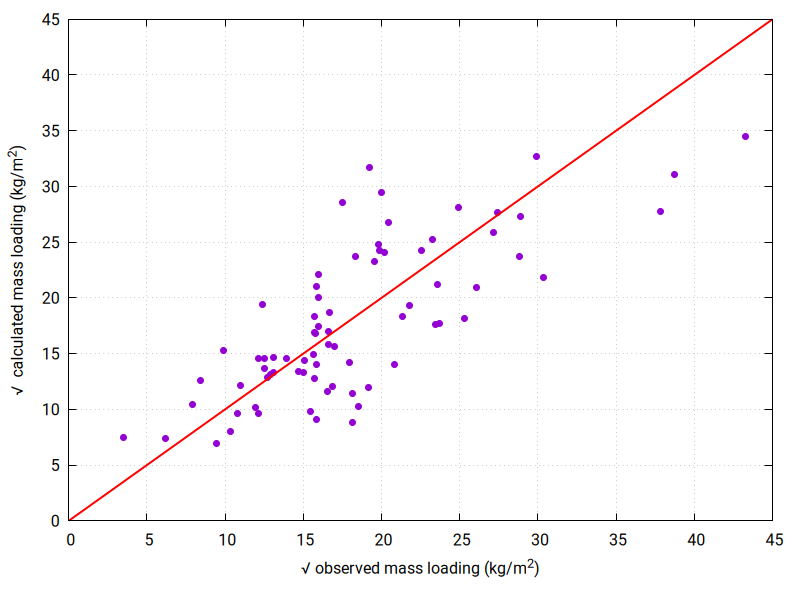
equiline style=

along with the percentage misfit between the observed mass loading and the calculated mass loading at each observation point:

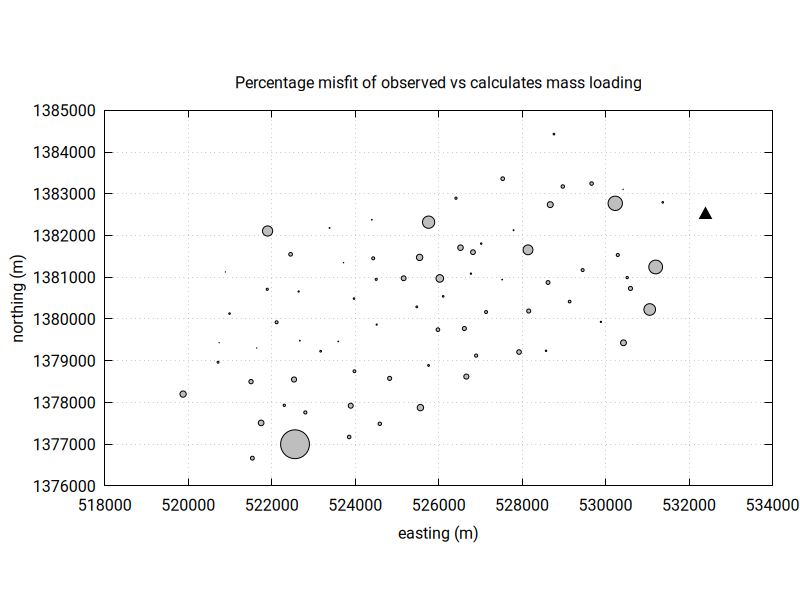
misfit

The eruption parameters for this model are:

  • eruption mass: 41108341352 kg (4.1e10)
  • maximum column height: 7313 m
  • alpha: 3.4
  • median deposit grainsize: 0.87 phi
So, this is a relatively large volume solution with a relatively fine median grainsize.

[Top]

Things to Try

  • Make sure you can download, compile and run the code. Running this code take some time (15 minutes?). Plot up the output to find the parameter ranges, central tendency in parameter values and any correlation among parameters.
  • In the current version of the code, the parameters are specified in main(). Try modifying the code so these parameter ranges are read from a configuration file. Hint: see the C shortcourse for an example of reading a configuration file: data4.c
[Top]

References

  • Connor, L.J. and Connor, C.B., 2006. Inversion is the key to dispersion: understanding eruption dynamics by inverting tephra fallout. Statistics in Volcanology, Geological Society of London, Special Publications, https://doi.org/10.1144/IAVCEI001.18. Inversion using the 1992 Cerro Negro eruption as an example. link to article
  • White, J.T., Connor, C.B., Connor, L. and Hasenaka, T., 2017. Efficient inversion and uncertainty quantification of a tephra fallout model. Journal of Geophysical Research: Solid Earth, 122(1), pp.281-294. Inversion of tephra fallout data from Cerro Negro and Kirishima eruptions using uncertainty quantification link to article
  • Mannen, K., Hasenaka, T., Higuchi, A., Kiyosugi, K. and Miyabuchi, Y., 2020. Simulations of tephra fall deposits from a bending eruption plume and the optimum model for particle release. Journal of Geophysical Research: Solid Earth, 125(6), p.e2019JB018902. Tephra2 inversion compared with a modified forward solution for a bent-over plume. link to article .
  • Yang, Q., Pitman, E.B., Bursik, M. and Jenkins, S.F., 2021. Tephra deposit inversion by coupling Tephra2 with the Metropolis-Hastings algorithm: algorithm introduction and demonstration with synthetic datasets. Journal of Applied Volcanology, 10, pp.1-24. Inversion using a Metropolis-Hastings algorithm. link to article .
  • Constantinescu, R., White, J.T., Connor, C.B., Hopulele‐Gligor, A., Charbonnier, S., Thouret, J.C., Lindsay, J.M. and Bertin, D., 2022. Uncertainty quantification of eruption source parameters estimated from tephra fall deposits. Geophysical Research Letters, 49(6), p.e2021GL097425. Inversion modeling larger eruptions with a modified forward solution. link to article