Gravity anomaly due to a dipping fault
Calculate the gravity anomaly due to a normal, reverse or thrust fault
Contents
Introduction
Code is provided to calculate the gravity anomaly due to a thin plate offset by a dipping fault, based on an analytical solution of the gravitational potential. The model assumes the plate is thin, and the gravitational attraction of the plate can be estimated by integrating along its length. That is, the gravitational attraction of a small mass on one side of the plate is not different from the gravitational attraction of a small mass on the opposite side of the plate.
This model can be a good representation of a normal, reverse or thrust fault, where a density contrast with the surrounding rock is created by offset of a horizontal unit.
Note that the dipping fault, normal in this case, creates lateral offset of the faulted unit. The faulted edges of the unit remain square, rather than reflecting the dip of the fault. This formulation assumes that the fault is linear, with the origin (x = 0) at the fault trace (intersection of the fault with the surface of the Earth). The plate is horizontal and of uniform thickness.
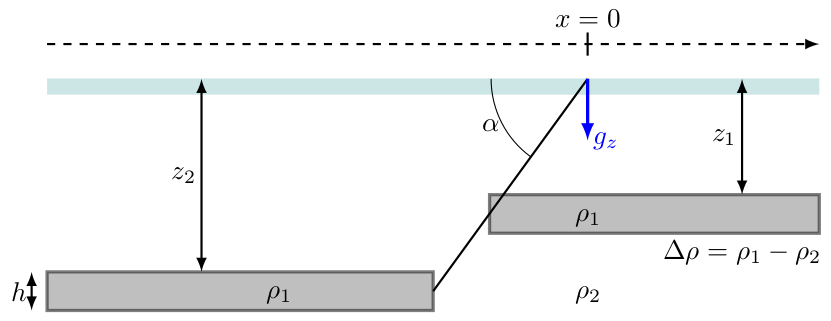
The faulted horizontal unit is assumed to extend infinitely in the $y$ direction (in and out of the $x-z$ plane). The faulted horizontal unit also extends infinitely in the $x$ direction, away from the fault. Far from the fault, the anomaly converges on the solution for the infinite slab, which depends on the unit thickness but not its depth.
Mathematical model
The gravity anomaly due to an offset horizontal unit across a dipping fault can be calculated using the following equation, $$g_z = 2 G \Delta \rho h \left (\pi + \tan^{-1}\left [\frac{x}{z_1} + \cot(\alpha)\right ] - \tan^{-1}\left [\frac{x}{z_2} + \cot(\alpha)\right ] \right )$$ where:
- $\alpha$ is the dip of the fault
- $z_1$ and $z_2$ are depths to the top of the faulted horizontal unit in the hanging wall and footwall of the fault, respectively
- $x$ is the horizontal offset from the intersection of the fault plane with the surface
- $h$ is the thickness of the horizontal unit
- $\Delta \rho$ is the density contrast between the faulted unit and surrounding rock
- $G$ is the gravitational constant.
Model assumptions
The model assumes that:
- The faulted plate extends infinitely in the strike direction (orthogonal to the $x-z$ plane).
- The faulted plate is thin. The thin plate is a good approximation to the prism if the thickness of the plate is less than the depth to the top of the plate.
- The plate is uniform and the density contrast between the plate and the surrounding rock (medium) is constant.
Calculate the gravity anomaly using perl
The following perl code calculates the gravity anomaly due to a horizontal plate offset by a dipping fault. The infinite slab anomaly, due to the plate being far from the fault, is subtracted, so the anomaly is calculated with respect to the Bouguer anomaly produced by the slab, which is not observable. The perl code uses two additional libraries that can be installed using the perl installer, cpan:
- Math::SigFigs
- Math::Trig
#!/usr/bin/perl
# command line USAGE: perl dipping_fault.pl > dipping_fault.dat
use warnings;
use strict;
use Math::SigFigs;
use Math::Trig;
$pi = 3.14159265358979;
my $fault_dip = 60.0 * $pi / 180.0; #radians
my $plate_depth_1 = 100; #m
my $plate_depth_2 = 500; #m
my $plate_thickness = 200; #m
my $plate_density_contrast = 500; #kg/m3
my $offset = 0.0;
my $gravity = 0.0;
for (my $i = 0; $i <= 200; $i++) {
$offset = ($i-100) * 25; #horizontal distance (m)
$gravity = gdip($fault_dip, $plate_depth_1, $plate_depth_2, $plate_thickness, $offset, $plate_density_contrast);
print "$offset ";
print FormatSigFigs($gravity,3),"\n";
}
sub gdip ($$$$$$) {
###########################################################################
#subroutine to calculate the gravity anomaly due to a horizontal plate
# cut by a dipping fault
# inputs:
# fault dip measured counter clockwise from surface (radians)
# depth to the top of the plate on the right and left sides of the fault (m)
# plate thickness (m)
# horizontal position of the gravity station relative to the fault trace (m)
# density contrast between plate and surrounding rock (m)
# output:
# gravity anomaly (mgal)
##########################################################################
my $alpha = shift; #fault dip (radians)
my $z_1 = shift; #depth of the plate right of fault (m)
my $z_2 = shift; #depth of the plate left of fault (m)
my $h = shift; #plate thickness (m)
my $x = shift; #input the horizontal distance of the
#location of the gravity observation (m)
my $del_density = shift; #input the density cotrast (kg/m3)
my $big_G = 6.67e-11; #gravitational const.
my $to_mgal = 1e5; #convert SI to mGal
my $angle1 = ($x/$z_1) + (cot($alpha));
my $angle2 = ($x/$z_2) + (cot($alpha));
my $grav = 2.0 * $to_mgal * $big_G * $del_density * $h * ($pi + atan($angle1) - atan($angle2));
$grav = $grav - 2.0 * $to_mgal * $big_G * $del_density * $h * $pi;
return $grav;
};
Plot the output using gnuplot
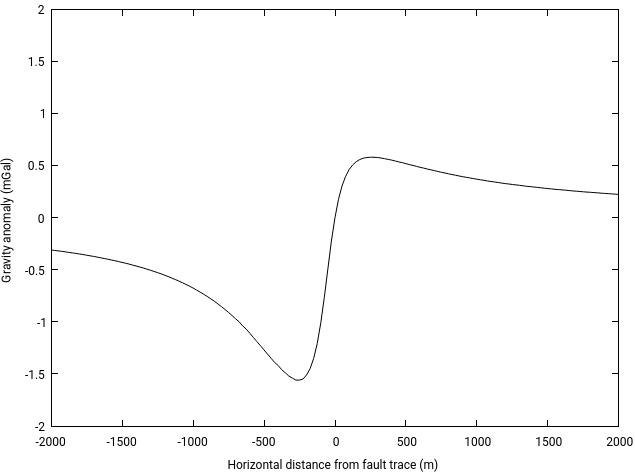
The gravity anomaly is not symmetric across the fault trace ($x=0$) because the dipping fault creates a gap in the horizontal unit at negative $x$ values. In this example, the plate is faulted by a normal fault, the horizontal plate to the left (x$ < 0$) is deeper than the horizontal plate to the right. The hanging wall of the fault is to the left of the fault trace, the footwall of the fault is to the right of the fault trace.
A gnuplot script is used to create this plot. This script requires an output file from the above perl script; the filename in the script is dipping_fault.dat.
# command line USAGE: gnuplot dipping_fault.gnu
# Be sure the output data file, dipping_fault.dat is located with this script
reset
set termoption dash
# Axes label
set xlabel 'Horizontal distance from fault trace (m)'
set ylabel 'Gravity anomaly (mGal)'
# Axes ranges
set xrange [-2000:2000]
set yrange [-2:2]
# Axes tics
set xtics 500
set ytics 0.5
set style fill transparent solid 0.15
set key Left
plot "dipping_fault.dat" using 1:2 with line lt rgb "black" notitle
set term pdf enhanced dashed
set output "dipping_fault_anomaly.pdf"
replot
Drawing with LaTeX and TikZ
The following LaTeX and TikZ code draws the figure of the model geometry presented at the top of the page.
\documentclass{article}
\usepackage{tikz}
\usetikzlibrary{calc,fadings,decorations.pathreplacing}
\usepackage{verbatim}
\usepackage{verbatim}
\usepackage[active,tightpage]{preview}
\PreviewEnvironment{tikzpicture}
\setlength\PreviewBorder{5pt}%
\tikzset{ %
>=latex, % option for nice arrows
inner sep=0pt,%
outer sep=2pt,%
mark coordinate/.style={inner sep=0pt,outer sep=0pt,minimum size=3pt,
fill=black,circle}%
}
\begin{document}
\begin{tikzpicture}
\draw[fill=gray, very thick, opacity=0.5] (-5,0) rectangle (0,0.5);
\draw[fill=gray, very thick, opacity=0.5] (0.73,1.0) rectangle (5,1.5);
\draw[teal, line width = 6, opacity = 0.2] (-5,2.9) -- (5,2.9) ;
\draw[thick] (2,3) -- (0,0.25);
\draw[<->, thick] (-3,0.5) --node[left] {$z_2$} (-3,3);
\draw[<->, thick] (4,1.5) --node[left] {$z_1$} (4,3);
% \draw[<->, thick] (0,3.1) --node[above] {$x$} (2,3.1);
\draw[<->, thick] (-5.2, 0) --node[left] {$h$} (-5.2,0.5);
\draw [black] (0.75,3) arc [radius=1.25, start angle=-180, end angle= -126];
\node at (0.75,2.4) {$\alpha$};
\node at (-2,0.2) {$\rho_1$};
\node at (2,1.2) {$\rho_1$};
\node at (2,0.2) {$\rho_2$};
\node at (4,0.75) {$\Delta \rho = \rho_1 - \rho_2$};
\draw[blue,->,very thick] (2,3) -- (2,2.2) node[right] {$g_z$};
\draw[thick] (2,3.3) -- (2,3.6) node[above] {$x=0$};
\draw[->,dashed, thick] (-5,3.45) -- (5,3.45);
\end{tikzpicture}
\end{document}
Some References
- Telford, W.M., Geldart, L.P. and Sheriff, R.E. (1990) Applied Geophysics, Cambridge University Press.
- MacMillan, W.D. (1958) The Theory of the Potential, Dover Books on Science and Engineering, New York.
Citation
Connor, C (2015) perl and gnuplot scripts for calculating and plotting the gravity anomaly due to a dipping fault.
Reference: https://gscommunitycodes.usf.edu/geoscicommunitycodes/public/geophysics/Gravity/dipping_fault.php