Gravity anomaly due to a 2D polygon
Calculate the gravity anomaly due to a 2D polygon in vertical cross section
Contents
Introduction
Manik Talwani developed a method for calculating the 2D gravity anomaly due to a polygon in vertical cross section as part of his dissertation at Columbia University in the 1950s. He and colleagues applied this method to interpret gravity anomalies associated with the Mendocino fracture zone off the coast of California and Oregon. Theirs was one of the first studies to successfully gather gravity measurements at sea, as well as to develop computational methods to calculate the gravity anomaly (Talwani et al., 1959).
The top part of the window shows a graph of the variation in gravity (mgal) as a function of distance (x) along a profile line. The bottom part of the window shows a simplified geologic cross section with horizontal distance (x) and depth (d). The polygon encloses an area of the cross-section with higher density than the surrounding rock. This density contrast creates a gravity anomaly.
Adjust the density contrast between the surrounding rock and the polygon using the slider. Drag the polygon vertices to change the size and shape of the polygon. Observe the change in the gravity anomaly calculated at each field point (shaded circles). If you drag a vertex across a polygon edge, you will violate this order and the gravity calculation will be incorrect.
Mathematical model
The model calculation uses a contour integral and Gauss's Law. The gravity anomaly is found by calculating the line integral along each polygon edge located between vertices in the polygon. The gravity anomaly due to the polygon is directly proportional to the sum of the line integrals and the density contrast between the polygon and the surrounding rock.
The polygon is 2D in the sense that it is assumed to extend infinitely in one direction. So, the calculation is appropriate for calculating gravity profiles that crosscut long geologic features.
Model assumptions
This model assumes that:- The line integral must proceed in a clockwise direction around the polygon. If this order is violated the gravity calculation will be incorrect.
- The polygon is completely buried within the subsurface.
- The polygon extends infinitely and perpendicular to the plane of the cross section (in and out of the computer screen, for example).
- The polygon is of uniform density and the density contrast with the surrounding rock is constant.
Model calculations
p5.js script
The interactive simulation above was drawn using this p5.js script:
Again, the polygon vertices must be entered in clockwise manner (counter-clockwise or random order will result in an error in the gravity calculation).
// Calculate the gravity anomaly due to a 2d polygon in cross section
// Chuck Connor
// 9/2018
// using the method of Manik Talwani and colleagues:
// Talwani et al (1959) Rapid gravity calculatons of two dimensional bodies...JGR 64:49-59.
// USAGE:
// Add these two script lines to the html header section:
// <script src="http://cdnjs.cloudflare.com/ajax/libs/p5.js/0.5.6/p5.js"><script>
// Here, the script source is stored with the html page
// <script src="talwani.js"><script>
//
// Add this div line to the html body section:
// <div id="sketch-holder" style="position: relative;"><div>
// The following is the script source code
var density_contrast = 500.0;
var x_zero = 50;
var x_scale = 100; //1 km = 50 screen units
var depth_zero = 200; //where the depth axis starts in screen units
var depth_scale = 100; //keep vert exaggeration 1:1
var mgal_zero = 170; //less than depth_zero
var mgal_scale = 10;
//create an array of corner objects
var corner = [];
//location of corner object
//these are global so mouse state can be checked
var x = [];
var y = [];
//number of corner objects
var num_corners;
//size of corner box
var boxSize = 5;
//keep track of mouse state for each corner object
//these are global so mouse state can be checked
var locked = [];
var overBox = [];
// i indexes corner objects
// this are global so mouse state can be checked
var i;
var densitySlider;
let myFont;
function preload() {
myFont = loadFont('talwani/p5/DejaVuSans.ttf');
}
function setup() {
var canvas = createCanvas(600, 480);
canvas.parent('sketch-holder');
stroke(0);
fill(0)
.strokeWeight(.30);
textFont(myFont, 16);
densitySlider = createSlider(1,255,0);
densitySlider.parent('sketch-holder');
densitySlider.position(450,20);
densitySlider.style('width', '80px');
densitySlider.parent('sketch-holder');
//noStroke();
rectMode(RADIUS);
//specify number and intial location of polygon corners
num_corners = 4;
x[0] = 300;
y[0] = 200;
x[1] = 500;
y[1] = 250;
x[2] = 300;
y[2] = 400;
x[3] = 100;
y[3] = 250;
//create corner objects and initialize mouse state for each corner
for (i=0; i x[i] - boxSize && mouseX < x[i] + boxSize &&
mouseY > y[i] - boxSize && mouseY < y[i] + boxSize) {
overBox[i] = true;
if (!locked[i]) {
fill(255);
}
} else {
overBox[i] = false;
}
}
this.display = function () {
// Draw the corner box and connecting line
if (locked[i] == true) {
boxSize = 10;
}else{
boxSize = 8;
};
fill('red');
rect(x[i], y[i], boxSize, boxSize);
if (i == num_corners-1) {
line(x[num_corners-1], y[num_corners-1], x[0], y[0]);
}else{
line(x[i], y[i], x[i+1], y[i+1]);
}
}
}
function mousePressed() {
//check the state f each corner, highlight slected corner
for (i=0; i width) {x[i]=width};
if (y[i] > height) {y[i]=height};
}
}
}
function mouseReleased() {
// no corner selected on mouse release
for (i = 0; i < num_corners; i++) {
locked[i] = false;
fill(255);
}
}
function talwani (x1,x2,z1,z2,density){
// assume that integration is clockwise
var G=6.67e-11;
var pi = 3.14159265358979;
var denom, alpha, beta, factor;
var r1sq, r2sq, term1, term2, zz, grav ;
//avoid singularites
if (x1 == 0) {x1=0.0001};
if (x2 == 0) {x2=0.0001};
if ((x2-x1)==0) {x2 = x1 - 0.0001};
denom = z2-z1;
if (denom == 0){denom = 1e-6};
alpha = (x2-x1)/denom;
beta = (x1*z2-x2*z1)/denom;
factor = beta/(1+alpha*alpha);
r1sq = (x1*x1 + z1 *z1);
r2sq = (x2*x2 + z2 *z2);
term1 = 0.5*(log(r2sq) - log(r1sq));
term2 = atan2(z2,x2)-atan2(z1,x1);
zz = factor*(term1-alpha*term2);
grav = 2*G*density*zz*1e5;
return grav; // return gravity in mgal
};
perl script
This perl script implements Talwani's solution of the gravity anomaly due to a 2D polygon. In this example, three vertex coordinates are used. More vertices can be added. The polygon vertices must be entered in clockwise manner (counter-clockwise or random order will result in an error in the gravity calculation). The output file is named output.dat. This file is used by the gnuplot script, below.
# USAGE:
# type: perl talwani.pl
# output file created by the code is named,
# output.dat
#######################################
# Function which
# calculates the gravity
# anomaly associated with one side of a 2D
# polygon (viewed in cross section and infinite
# in and out of plane of screen).
# INPUTS:
# x1, x2, z1, z2, density;
# in this order!
# OUTPUT:
# gravity in mGals
########################################
sub talwani ($$$$$){
my $x1= shift; #meters
my $x2= shift;
my $z1= shift ;
my $z2= shift;
my $del_density = shift;
# assume that integration is clockwise
my $G=6.67e-11;
my $pi = 3.14159265358979;
# avoid singularites
if ($x1 == 0) {$x1 = 0.0001};
if ($x2 == 0) {$x2 = 0.0001};
if (($x2 - $x1) == 0) {$x2 = $x1 - 0.0001};
my $denom = $z2 - $z1;
if ($denom == 0){$denom = 1e-6};
my $alpha = ($x2 - $x1)/$denom;
my $beta = ($x1 * $z2 - $x2 * $z1)/$denom;
my $factor = $beta/(1 + $alpha*$alpha);
my $r1sq = ($x1*$x1 + $z1 * $z1);
my $r2sq = ($x2*$x2 + $z2 * $z2);
my $term1 = 0.5 * (log($r2sq) - log($r1sq));
my $term2 = atan2($z2, $x2) - atan2($z1, $x1);
my $zz = $factor * ($term1 - $alpha * $term2);
$grav = 2 * $G * $del_density * $zz * 1e5;
return $grav; # return gravity in mgal
};
###########Main Program ##################
# Open an output file
open OUTPUT, "> outfile.dat " or die "Can't open output file 1: $!";
# create the polygon
# vertices must be
# in clockwise order!
$x[0] = 0;
$z[0] = 50;
$x[1] = 275;
$z[1] = 50;
$x[2] = 90;
$z[2] = 200;
$density_contrast = 1000;
$n = 3; # number of polygon sides
for ($offset = -300; $offset < 500; $offset += 25){
for ($i = 0; $i < $n; $i++) {
if($i == $n-1) {
$i2=0
} else {
$i2=$i+1
};
$x1 = $x[$i]-$offset;
$x2 = $x[$i2]-$offset;
$z1 = $z[$i];
$z2 = $z[$i2];
$gravity += talwani($x1, $x2, $z1, $z2, $density_contrast);
};
print OUTPUT "$offset $gravity\n";
$gravity = 0;
};
Example Output
Below, are some lines from the output file produced by the PERL script:
-300 0.151642927177365
-275 0.170683413517453
-250 0.19347869702967
-225 0.221063635117057
-200 0.254847118921216
-175 0.296782005330622
-150 0.349628244608359
-125 0.417366262746836
-100 0.505845010404403
-75 0.6237373432899
-50 0.783530160775372
-25 1.00008560680416
0 1.27691259801489
Below, is a list of example vertices. The first column is the x coordinate of each vertex; the second column is the corresponding depth of each vertex. Notice that the first and last vertex must have the same x coordinate and depth value in order to close the polygon.
0 50
275 50
90 200
0 50
Plotting the output using gnuplot
The output from the perl script is plotted below. Plot A is the gravity anomaly (in mGals) due to the polygon drawn in plot B. 0 meter depth represents the ground surface. The polygon represents a slice through an object that extends into and out-of the screen.
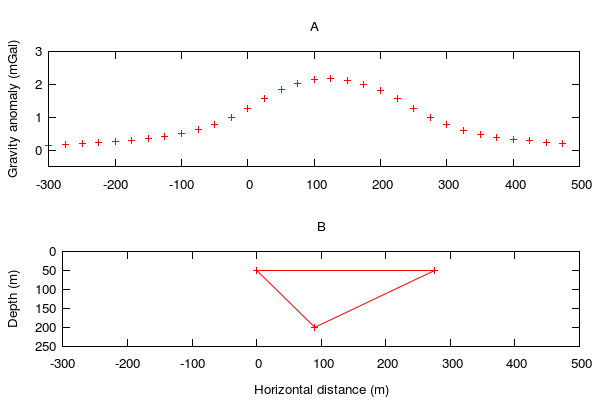
The gnuplot script requires two files to run, the output file produced by the perl script, output.dat, and a vertex file, vertex.dat. Example files are shown above.
# USAGE:
# type: gnuplot talwani.gnu
# on the command line
# script requires 2 data files:
# outfile.dat and vertex.dat
reset
set terminal pngcairo enhanced font "arial,10" fontscale 1.0 size 600, 400
set output 'talwani.png'
set multiplot layout 2,1
# Axes label
set ylabel 'Gravity anomaly (mGal)'
# Axes ranges
set xrange [-300:500]
set yrange [-0.5:3]
# Axes tics
set xtics 100
set ytics 1
set title 'A'
plot "outfile.dat" using 1:2 with points lt rgb "red" notitle
set xlabel 'Horizontal distance (m)'
set ylabel 'Depth (m)'
set yrange [250:0]
set ytics 50
set title 'B'
plot "vertex.dat" using 1:2 with linespoints lt rgb "red" notitle
Some References
- Talwani et al. (1959) Rapid gravity computations for two - dimensional bodies with application to the Mendocino submarine fracture zone, Journal of Geophysical Research 64(1):49-59.
- Telford, W.M., Geldart, L.P. and Sheriff, R.E. (1990) Applied Geophysics, Cambridge University Press.
- MacMillan, W.D. (1958) The Theory of the Potential, Dover Books on Science and Engineering, New York.