Gravity Anomaly Due to a Vertical Fault
Calculate the gravity anomaly due to a vertical fault that offsets a horizontal plate
Contents
Introduction
Code is provided to calculate the gravity anomaly due to a horizontal plate cut by a vertical fault resulting in some vertical offset of the plate. The solution is based on an analytical solution of the gravitational potential. The model assumes the plate is thin, and the gravitational attraction of the plate can be estimated by integrating along its length. That is, the gravitational attraction of a small mass on the top side of the plate is not different from the gravitational attraction of a small mass on the bottom side of the plate.
A plate offset by a vertical fault can be a good surrogate for anomalies identified along some strike-slip faults, which can create change in the depth to some units across the fault, creating a density contrast with the surrounding rock.
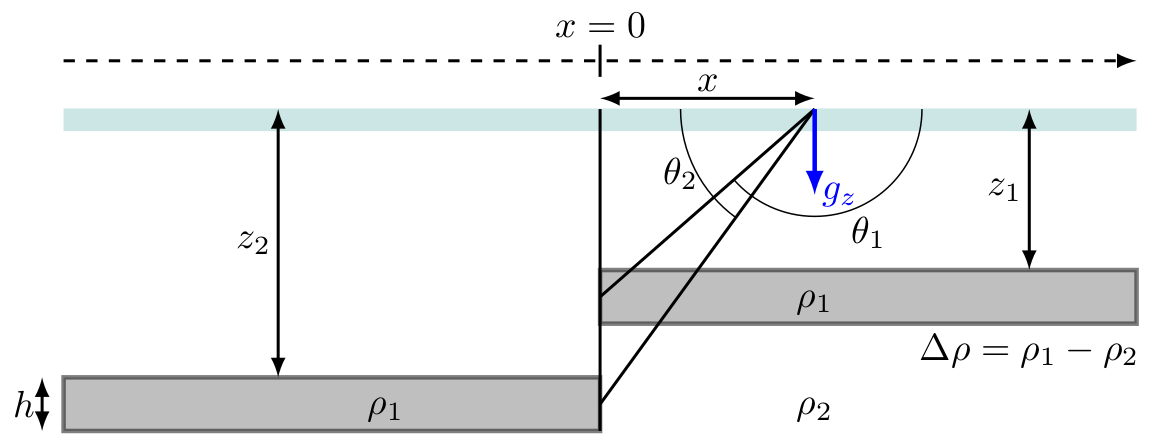
Mathematical model
The gravity anomaly due to an offset of a horizontal unit across a vertical fault can be expressed mathematically, $$g_z = 2 G \Delta \rho h \left (\pi + \tan^{-1}\left [\frac{x}{z_1}\right ] - \tan^{-1}\left [\frac{x}{z_2}\right ] \right )$$ where:
- $z_1$ and $z_2$ are depths to the top of the faulted horizontal unit
- $x$ is the horizontal offset from the intersection of the fault plane with the surface
- $h$ is the thickness of the faulted horizontal unit
- $\Delta \rho$ is the density contrast between the faulted horizontal unit and surrounding rock
- $G$ is the gravitational constant.
This expression can also be written as, $$g_z = 2 G \Delta \rho h \left [\theta_1 + \theta_2 \right ]$$ where, $$\theta_1 = \frac{\pi}{2}+ \tan^{-1} \frac{x}{z_1}$$ $$\theta_2 = \frac{\pi}{2}- \tan^{-1} \frac{x}{z_2}$$ The angles are shown in the figure at the top of the page.
The faulted horizontal unit is assumed to extend infinitely in the $y$ direction (in and out of the $x-z$ plane). The faulted horizontal unit also extends infinitely in the $x$ direction, away from the fault.
Model Assumptions
The model assumes that:
- The faulted plate extends infinitely in the strike direction (orthogonal to the $x-z$ plane)
- The faulted plate is thin. The thin plate is a good approximation to the prism if the thickness of the plate is less than the depth to the top of the plate.
- The plate is uniform and the density contrast between the plate and the surrounding rock (medium) is constant.
Calculate the gravity using perl
The following perl code calculates the gravity anomaly due to a faulted horizontal plate, where the plate is cut by a vertical fault. The model uses a thin plate approximation. The perl code uses two additional libraries that can be installed using the perl installer, cpan.
- Math::SigFigs
- Math::Trig
This code subtracts the anomaly due to the infinite slab, so the anomaly tends to 0 mGal with increasing distance from the fault trace.
#!/usr/bin/perl,
# Calculate the gravity anomaly
# due to horizontal plate offset by
# a vertical fault.
use warnings;
use strict;
use Math::SigFigs;
use Math::Trig;
my $pi = 3.14159265358979;
# Set up some model inputs
my $plate_depth_1 = 50; #m
my $plate_depth_2 = 100; #m
my $plate_thickness = 100; #m
my $plate_density_contrast = 800; #kg/m3
my $offset = 0.0;
my $gravity = 0.0;
for (my $i=0; $i<=200; $i++) {
# horizontal distance (m)
$offset = ($i-100) * 25;
$gravity = gvert_fault($plate_depth_1, $plate_depth_2, $plate_thickness, $offset, $plate_density_contrast);
print "$offset ";
print FormatSigFigs($gravity,3), "\n";
}
###########################################################################
# subroutine to calculate the gravity anomaly due to a horizontal plate
# cut by a vertical fault.
# inputs:
#
# depth to the top of the plate on the right and left sides of the fault (m)
# plate thickness (m)
# horizontal position of the gravity station relative to the fault trace (m)
# density contrast between plate and surrounding rock (m)
# output:
# gravity anomaly (mgal)
##########################################################################
sub gvert_fault ($$$$$) {
my $pi = 3.14159265358979;
# (input) depth of the plate right of fault (m)
my $z_1 = shift;
# (input) depth of the plate left of fault (m)
my $z_2 = shift;
# (input) plate thickness (m)
my $h = shift;
# (input) horizontal distance of the
# location of the gravity observation (m)
my $x = shift;
# (input) density contrast (kg/m3)
my $del_density = shift;
# gravitational constant
my $big_G = 6.67e-11;
# convert SI to mGal
my $to_mgal = 1e5; #convert SI to mGal
my $angle1 = ($x/$z_1);
my $angle2 = ($x/$z_2);
my $grav = 2.0 * $to_mgal * $big_G * $del_density * $h * ($pi + atan($angle1) - atan($angle2));
$grav = $grav - 2.0 * $to_mgal * $big_G * $del_density * $h * $pi;
return $grav;
};
Plot the output using gnuplot
The above code, using some example parameters, yields the following output when graphed.
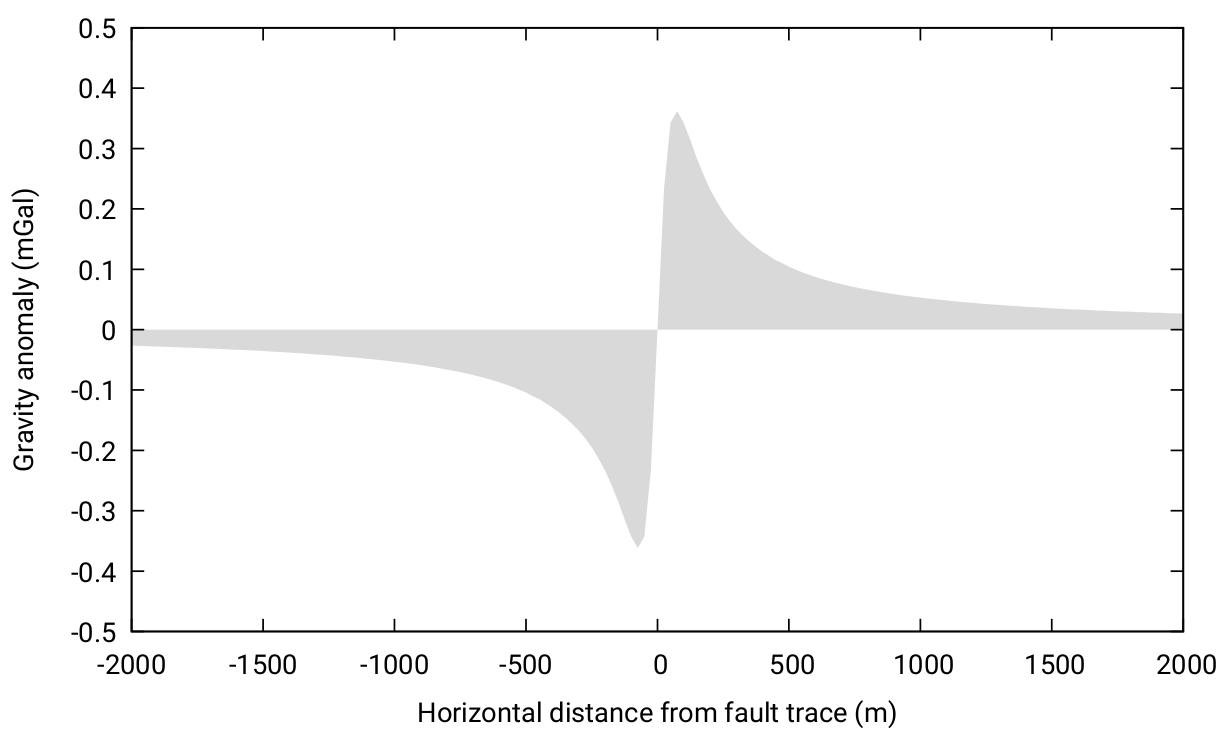
A gnuplot script is used to create this plot. The script assumes that the output generated by the above perl script is stored in the file, vertical_fault.dat.
# USAGE: gnuplot vert_fault.gnu
reset
set termoption dash
# Axes label
set xlabel 'Horizontal distance from fault trace (m)'
set ylabel 'Gravity anomaly (mGal)'
# Axes ranges
set xrange [-2000:2000]
set yrange [-0.5:0.5]
# Axes tics
set xtics 500
set ytics 0.1
set style fill transparent solid 0.15
set key Left
plot "vertical_fault.dat" using 1:2 with filledcurve y1=0 lt rgb "gray0" notitle"
set term pdf enhanced dashed
set output "vertical_fault_anomaly.pdf"
replot
Drawing with LaTeX and TikZ
The following LaTeX and TikZ script draws the figure of the model geometry presented at the top of the page.
\documentclass{article}
\usepackage{tikz}
\usetikzlibrary{calc,fadings,decorations.pathreplacing}
\usepackage{verbatim}
\usepackage{verbatim}
\usepackage[active,tightpage]{preview}
\PreviewEnvironment{tikzpicture}
\setlength\PreviewBorder{5pt}%
\tikzset{%
>=latex, % option for nice arrows
inner sep=0pt,%
outer sep=2pt,%
mark coordinate/.style={inner sep=0pt,outer sep=0pt,minimum size=3pt,
fill=black,circle}%
}
\begin{document}
\begin{tikzpicture}
\draw[fill=gray, very thick, opacity=0.5] (-5,0) rectangle (0,0.5);
\draw[fill=gray, very thick, opacity=0.5] (0,1.0) rectangle (5,1.5);
\draw[teal, line width = 6, opacity = 0.2] (-5,2.9) -- (5,2.9) ;
\draw[thick] (0,0) -- (0,3);
\draw[thick] (2,3) -- (0,0.25);
\draw[thick] (2,3) -- (0,1.25);
\draw[<->, thick] (-3,0.5) --node[left] {$z_2$} (-3,3);
\draw[<->, thick] (4,1.5) --node[left] {$z_1$} (4,3);
\draw[<->, thick] (0,3.1) --node[above] {$x$} (2,3.1);
\draw[<->, thick] (-5.2, 0) --node[left] {$h$} (-5.2,0.5);
\draw [black] (3,3) arc [radius=1, start angle=0, end angle= -139];
\draw [black] (0.75,3) arc [radius=1.25, start angle=-180, end angle= -126];
\node at (2.5,1.85) {$\theta_1$};
\node at (0.75,2.4) {$\theta_2$};
\node at (-2,0.2) {$\rho_1$};
\node at (2,1.2) {$\rho_1$};
\node at (2,0.2) {$\rho_2$};
\node at (4,0.75) {$\Delta \rho = \rho_1 - \rho_2$};
\draw[blue,->,very thick] (2,3) -- (2,2.2) node[right] {$g_z$};
\draw[thick] (0,3.3) -- (0,3.6) node[above] {$x=0$};
\draw[->,dashed, thick] (-5,3.45) -- (5,3.45);
\end{tikzpicture}
\end{document}
Some References
- Telford, W.M., Geldart, L.P. and Sheriff, R.E. (1990) Applied Geophysics. Cambridge University Press.
- MacMillan, W.D. (1958) The Theory of the Potential, Dover Books on Science and Engineering, New York.