Magnetic anomaly due to a dipole
Calculate the magnetic anomaly due to a buried sphere using the magnetic dipole moment
Contents
Introduction
Naturally occurring magnetic anomalies are caused by variations in the magnetic properties of rocks. The magnitude of the magnetic anomaly caused by a rock depends, in part, on how magnetic the rock is, which is summarized by a parameter called rock magnetization. Rock magnetization describes how strong a magnetic anomaly will be at a given distance from the rock, per unit volume of the magnetized rock body. Magnetization is a vector with orientation and magnitude. The vector of magnetization depends on a variety of factors including mineralogy, grain size, chemical alteration and thermal history of the rock. The vector of magnetization also depends on the strength or magnitude of the external magnetic field, e.g., Earth's magnetic field, that contains the rock. The magnitude of the vector of magnetization, the intensity of magnetization, and has units of amp/m.
For simple geometries, like a bar magnet or a buried sphere, the vector of magnetization can by multiplied by the volume of the rock to calculate the magnetic dipole moment, also a vector, which describes the amplitude of the magnetic anomaly at a given distance, $$\vec \mu = \vec M V$$ where $\vec \mu$ is the magnetic dipole moment, $\vec M$ is the rock magnetization, and $V$ is the volume of magnetized rock. The vector of magnetization, $\vec M$, can be measured in a lab using a sample of rock from the magnetized body. The magnetic dipole moment, $\vec \mu$, depends on the rock magnetization $\vec M$ and on the volume and shape of the whole rock mass.
The vector of magnetization, $\vec M$ has three components, $M_x$ in the east direction, $M_y$ in the north direction, and $M_z$ in the vertical (downward) direction. The orientation of this vector is measured as inclination $M_I$ (angle with respect to horizontal, positive downward), and declination $M_D$ (angle with respect to geographic north, positive in clockwise direction), with magnitude $| \vec M|$.
In the presence of an external magnetic field $\vec H$, e.g., Earth's magnetic field, the rock magnetization, $\vec M$, is a function of the rock's magnetic susceptibility $k$ and $\vec H$, the external magnetic field. The magnetic susceptibility, $k$, can be thought of as the fraction of the rock volume that contained minerals, or more specifically mineral domains, that create their own magnetic field in the presence of an external magnetic field. Rocks, especially igneous rocks, often acquire remanent magnetization as they cool and crystallize. Remanent magnetization is added to get the rock's total vector of magnetization, $$ \vec M = \vec M_R + k \vec H$$ where $\vec M_R$ is the remanent magnetization (amp/m), $k$ is the magnetic susceptibility (dimensionless ratio) and $\vec H$ is the external magnetic field. Note that if the external magnetic field is zero, the vector of magnetization only depends on the remanent magnetization.
Above, is a visual representation of the magnetic anomaly due to a buried magnetized sphere, a simple magnetic dipole. The sphere is shown as a gray circle in cross section, and has a radius, $a$. The sphere is a simple symmetric shape, so the magnetic dipole moment is equal to the sphere's magnetization times the sphere volume, $$ \vec \mu = \vec M \frac{4}{3} \pi a^3.$$
The vector of magnetization $\vec M$ is shown by the black arrow within the gray circle. $\vec M$ can be altered by changing its direction and magnitude using the sliders, which corresponds to changing the sphere's rock magnetic properties, or changing its inclination. By changing the vector of magnetization, the value of the magnetic dipole moment changes. The change in the magnetic dipole moment is used to calculate the change in the magnetic anomaly (in units of nanoTesla, nT) observed at the surface (plotted in red), using equations that are provided in the following. Move the sphere using the mouse to change its location or use the slider to change the sphere's radius and notice the change in the magnetic anomaly.
The calculation of the magnetic anomaly due to the buried sphere using its magnetic dipole moment is implemented in p5.js javascript code (see code below). This simplified code assumes that the vector of magnetization is in the direction of Earth's magnetic field (shown as normal, South to North along the x axis).
Other simple shapes can be approximated with a magnetic dipole using different equations for the volume and even by adding magnetic dipoles together. The dipole model does not work for complex shapes calculated at relatively short distances, such as a long plate-like body.
Mathematical Model
The diagram below shows a sphere (our magnetic dipole) located below the surface (teal line) and centered at point $O$. $P$ represents a place of measurement at the surface. $P$ is located $r$ meters away from $O$, the center of the magnetic dipole, with $r_x$, $r_y$, and $r_z$ representing the $x$, $y$, and $z$ components of this distance, respectively, and $a$ indicating the radius of the sphere. The image shows a 3D perspective, with the surface line parallel to the N–S direction ($y$-axis), the E–W direction ($x$-axis) extending into and out of the screen, and the $z$-axis extending vertically downward. The vector $\vec \mu$, the magnetic dipole moment, is shown in red.
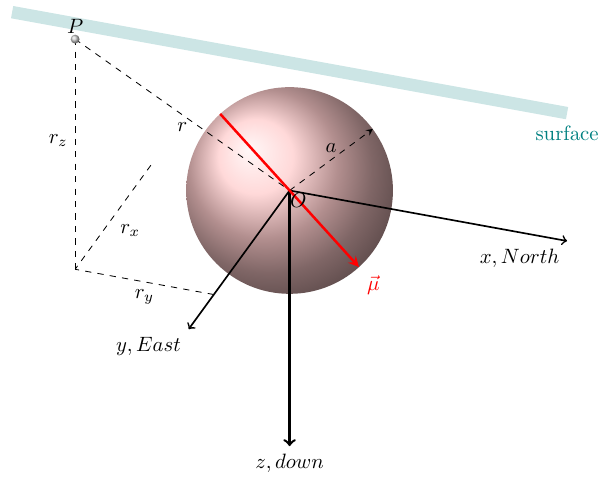
- $|\vec M|$ is the intensity or magnitude of the vector of magnetization (in amp/m)
- $M_{I}$ is the inclination of the magnetization (in radians, measured positive down from the surface)
- $M_{D}$ is the declination of the magnetization (in radians, measured positive to the east)
Given these vectors and direction cosines, the magnetic anomaly due to the magnetized sphere, can be calculated for the $x$, $y$, and $z$ directions, taking into account $r$, the distance of the measurement point $P$ from the center of the buried sphere $O$. This calculation relies on the dot product of the vector of magnetization and the distance of the dipole from the measurement location $\vec r$, $$\vec M \cdot \vec r = M_x r_x + M_y r_y + M_y r_z$$
The components of the total magnetic anomaly $B$ (measured at point $P$) are as follows, \begin{align} B_x & = 400 \pi |\vec \mu| \frac{3 (\vec M \cdot \vec r) r_x-r^2*M_x}{r^5}\\ B_y & = 400 \pi |\vec \mu| \frac{3 (\vec M \cdot \vec r) r_y-r^2*M_y}{r^5}\\ B_z & = 400 \pi |\vec \mu| \frac{3 (\vec M \cdot \vec r) r_z-r^2*M_z}{r^5} \end{align} where $|\vec \mu|$ is the magnitude of the dipole vector, $$|\vec \mu| = |\vec M| \frac{4}{3} \pi a^3$$
The normalized external magnetic field $E$ (e.g., Earth's magnetic field) has an inclination and declination based on location, with components (called direction cosines) that are calculated as follows, \begin{align} E_x & = \cos(E_{I}) \times \cos (E_D)\\ E_y & = \cos(E_{I}) \times \sin (E_D)\\ E_z & = \sin(E_{I}) \end{align} where:
- $E_{I}$ is the inclination of the $E$, measured in radians, positive down from horizontal
- $E_D$ is the declination of $E$, measured in radians, positive to the east
- $E$ is normalized having a magnitude equal to 1
Computationally, if the magnitude of the external magnetic field is specified in units of nanoTesla (nT), a proportionality constant is used to convert it to units of magnetization (amp/m) which depend on the magnetic permeability $\mu_o$. If the magnetic permeability is $\mu_o = 4 \pi \times 10^{-7}$ m T/amp, and 1 T = $1 \times 10^9$ nT, the proportionality constant used to express the magnetic anomaly caused by the rock in units of nanoTesla (nT) when magnetization is expressed in amp/m, is $400 \pi$.
Model assumptions
This model assumes that:- The depth ($r_z$) to the center of the sphere ($O$) is greater than the sphere radius ($a$).
- The sphere is uniformly magnetized and the magnetization contrast between the sphere and the surrounding rock (or other material) is constant.
- The magnetic anomaly due to the sphere is much smaller than the intensity (field strength) of the external magnetic field.
Model calculations
[Top]p5.js script
The interactive simulation above was drawn using this p5.js script:
// C. B. Connor; Feb 2020
// magnetic anomaly due to a buried sphere
// used as a magnetic dipole
// The code assumes that the vector of magnetization is in the direction
// of the external field, and there is zero declination.
// The profile is drawn on a N-S line through the center of the sphere.
// USAGE:
// Add these two script lines to the html header section:
// <script src="http://cdnjs.cloudflare.com/ajax/libs/p5.js/0.5.6/p5.js"><script>
// Here, the script source is stored with the html page
// <script src="magsphere.js"><script>
//
// Add this div line to the html body section:
// <div id="sketch-holder" style="position: relative;"><div>
// What follows is the script source code,
// the contents of magsphere.js
//graph scales and axes positions
var x = 200;
var y = 300;
var radius = 50; //in screen units, 1 km = 100 screen units
var x_zero = 50;
var x_scale = 1; //1 km = 1 screen units
var depth_zero = 210; //where the depth axis starts in screen units
var depth_scale = 1; //keep vert exaggeration 1:1
var mag_zero = 110; //less than depth_zero
var mag_scale = 1;
//initialize magnetic field variables
var PI = 3.14159;
var DEG2RAD = 0.017453293;
var INC_EARTH_MAG_FIELD = 45.0;
var DEC_EARTH_MAG_FIELD = 0.0;
var PROP = 400 * PI;
var INTENSITY = 0.25; // Am^-1
var INC_VECTOR_OF_MAG = 45.0; //prob parallel to earth field unless reversed
var DEC_VECTOR_OF_MAG = 0.0; // prob parallel to eath field unless rotated or reversed
var incSlider;
var intensitySlider;
var volumeSlider;
var inc_arrow;
over = false,
move = false;
let myFont;
function preload() {
myFont = loadFont('dipole/p5/DejaVuSans.ttf');
}
function setup() {
var canvas = createCanvas(600,480);
// Move the canvas so it's inside our .
canvas.parent('sketch-holder');
stroke(0);
fill(0)
.strokeWeight(.30);
textFont(myFont, 16);
incSlider = createSlider(0, 255, 200);
incSlider.position(275, 450);
incSlider.style('width', '100px');
incSlider.parent('sketch-holder');
intensitySlider = createSlider(0, 255, 200);
intensitySlider.position(445, 450);
intensitySlider.style('width', '100px');
intensitySlider.parent('sketch-holder');
volumeSlider = createSlider(0, 255, 200);
volumeSlider.position(100, 450);
volumeSlider.style('width', '100px');
volumeSlider.parent('sketch-holder');
rectMode(CORNERS);
smooth();
inc_arrow = new Arrow();
}
function draw() {
background('#CFC493');
var anomaly;
var del_mag;
var offset;
var x1, y1, z1, m;
var x1km, y1km, r;
// check in on the slider bar for inclination values
INC_VECTOR_OF_MAG = -90 + incSlider.value()/255*180;
INC_EARTH_MAG_FIELD = INC_VECTOR_OF_MAG;
INTENSITY = 0 + intensitySlider.value()/255*0.25;
radius = 10 + volumeSlider.value()/255*100.0;
// check in for box movement and update position
updatebox();
drawbox();
//calculate and draw magnetic anomaly
for (offset = x_zero; offset < width; offset += 2){
//count in screen units
xposition = (offset-x_zero); //distance in meters from edge
yposition = 0;
x1 = (x) - offset;
z1 = (y);
x1km = x1/x_scale*1000.0;
y1km = (z1 - depth_zero)/depth_scale*1000.0;
r = 4/3 * PI * (radius/x_scale*1000.0)**3;
//r = 4/3 * PI * r**3;
//anomaly uses calcMag to find the magnetic anomaly
anomaly = calcMag(r, x1km, y1km);
// convert mag anomaly to integer
del_mag = anomaly*mag_scale;
m = mag_zero - del_mag;
// plot point
stroke(0);
fill('red');
ellipse(offset,m, 5, 5);
}
//draw axes and labels
drawAxes(x_zero, x_scale, depth_zero, depth_scale, mag_zero, mag_scale);
}
function drawAxes(x_zero, x_scale, depth_zero, depth_scale, mag_zero, mag_scale) {
fill(0);
stroke(0);
//draw and label depth axis
textSize(12);
textAlign(RIGHT);
for (var i = 0; i < 7; i++) {
var d1 = i * 50;
var d = d1 * depth_scale + depth_zero;
line(x_zero, d, x_zero - 10, d);
text(d1, x_zero - 12, d + 5);
}
//draw and label mgal axis
textAlign(RIGHT);
for (var i = -5; i < 10; i++) {
var d = mag_zero - 20 * i * mag_scale;
line(x_zero, d, x_zero-10, d);
text(i * 20, x_zero - 12, d + 5);
}
//draw label the horizontal axis
textAlign(CENTER);
for (var i = 1; i < 11; i++) {
var x1 = i * 50;
var x=x1 * x_scale + x_zero;
line(x, depth_zero-35, x, depth_zero - 25);
line(x, depth_zero-5, x, depth_zero + 5);
var x_value = x1;
text(x_value, x, depth_zero - 10);
}
// rotate(3.14159/2.0);
textAlign(CENTER);
text("depth (m)", 100, 250);
//depth arrow
line(95, 255, 95, 300);
triangle(90,300,100,300,95,325);
text("horizontal distance (m)", 440, 250);
//horiontal arrow
line(520, 245, 555, 245);
triangle(555,240,555,250,580,245);
text("mag (nT)", 85, 50);
text("North", 550, depth_zero-50);
text("South", 100, depth_zero-50);
text("Inclination (deg):", 325, 440);
text(nfc(INC_VECTOR_OF_MAG, 2), 400, 460);
text("Intensity (amp/m):", 500, 440);
text(nfc(INTENSITY, 2), 580, 460);
text("Radius (m):", 135, 440);
text(nfc(radius, 2), 225, 460);
}
function drawbox() {
// Set color and draw top bar
if (over || move) {
fill(255);
} else {
fill(204);
}
if (x < x_zero+radius) {x = x_zero+radius;}
if (x > width - radius) {x = width - radius;}
if (y < depth_zero+radius) {y = depth_zero+radius;}
if (y > height-radius) {y = height-radius;}
ellipse(x, y, 2*radius, 2*radius);
inc_arrow.update();
}
function updatebox() {
// Test if mouse if over the sphere
if (mouseX > x-radius && mouseX < x+radius && mouseY > y-radius && mouseY < y+radius) {
over = true;
} else {
over = false;
}
// Set and constrain the position of top bar
if (move) {
x = mouseX;
y = mouseY;
}
}
function mousePressed() {
if (over) {
move = true;
}
}
function mouseReleased() {
move = false;
}
function Arrow(){
this.update = function() {
var angle = DEG2RAD * INC_VECTOR_OF_MAG;
var length = INTENSITY*20;
push();
translate(x,y);
rotate(angle);
fill(0);
beginShape()
noStroke();
vertex(-9*length,-length);
vertex(5*length, -length);
vertex(5*length, -3*length);
vertex(9*length, 0);
vertex(5*length, 3*length);
vertex(5*length, length);
vertex(-9*length,length);
endShape(CLOSE);
pop();
}
}
function calcMag(aa,xx,zz) {
var einc = DEG2RAD * INC_EARTH_MAG_FIELD;
var edec = DEG2RAD * DEC_EARTH_MAG_FIELD;
var mi = INTENSITY;
var minc = DEG2RAD * INC_VECTOR_OF_MAG;
var mdec = DEG2RAD * DEC_VECTOR_OF_MAG;
var prop = PROP;
//calculate direction cosines for magnetiation
var ml = cos(minc) * cos(mdec);
var mm = cos(minc) * sin(mdec);
var mn = sin(minc);
//calculate the dipole moment assuming a sphere shape
//notice this scales linearly with the
//intensity of magnetization
//var dpm = 4/3 * PI * aa**3 * mi;
var dpm = aa * mi;
//components of magnetization in x,z directions
var mx = mi * ml;
var mz = mi * mn;
var el = cos(einc) * cos(edec);
var en = sin(einc);
var r2 = xx**2 + zz**2;
var r = sqrt(r2);
var r5 = r**5;
var dotprod = xx*mx + zz*mz;
//components of the anomalous magnetic field
var bx = prop*dpm*(3*dotprod*xx-r2*mx)/r5;
var bz = prop*dpm*(3*dotprod*zz-r2*mz)/r5;
//calculate total anomaly
//this calculation works for anomaly << total field strength
var b_total = el*bx + en*bz;
return b_total;
}
perl script
This perl script calculates the magnetic anomaly due to a buried sphere used as a magnetic dipole. The code calculates along a N-S profile line. Output is the magnetic anomaly in nT. The output file is named dipole.dat. This file is used by the gnuplot script, below.
# Calculate the magnetic anomaly due to a buried magnetized sphere
# USAGE:
# type: perl dipole.pl > dipole.dat
# output file is named dipole.dat
$pi = 3.14159;
#sphere is centered at point (0,0,z)
#set depth of center > 0
$z = 100; #meter
#set the radius < $z
$a = 50; #meter
#set magnetization (amp/m)
$minc = 45*$pi/180; #inclination down in rad
$mdec = 0*$pi/180; #declination east in rad
$mi = 1; #intensity of magnetization (amp/m)
#calculate direction cosines for magnetiation
$ml = cos($minc) * cos($mdec);
$mm = cos($minc) * sin($mdec);
$mn = sin($minc);
#calculate the dipole moment assuming a sphere shape
#notice this scales linearly with the
#intensity of magnetization
$dpm = 4/3 * $pi * $a**3 * $mi;
#components of magnetization in x,y,z directions
$mx = $mi * $ml;
$my = $mi * $mm;
$mz = $mi * $mn;
#set earth's field
$einc = 45*$pi/180; #inclination down in rad
$edec = 0*$pi/180; #declination east in rad
$el = cos($einc) * cos($edec);
$em = cos($einc) * sin($edec);
$en = sin($einc);
#proportionality constant is
# magnetic permeability * 1e9
#to convert of nT
$prop = 400*$pi;
for ($j =0; $j<400; $j++) {
#px is the northing of the observation point
#py is the easting of the observation point
$px = $j-200;
$py = 0;
$pz = -$z;
$r2 = $px**2 + $py**2 + $pz**2;
$r = sqrt($r2);
$r5 = $r**5;
$dotprod = $px*$mx + $py*$my + $pz*$mz;
#components of the anomalous magnetic field
$bx = $prop*$dpm*(3*$dotprod*$px-$r2*$mx)/$r5;
$by = $prop*$dpm*(3*$dotprod*$py-$r2*$my)/$r5;
$bz = $prop*$dpm*(3*$dotprod*$pz-$r2*$mz)/$r5;
#calculate total anomaly
#this calculation works for anomaly << total field strength
$b_total = $el*$bx + $em*$by + $en*$bz;
#print results
print " $px $b_total\n";
}
Plot the output using gnuplot
The output from the perl script is plotted below. Shown is the magnetic anomaly (red line) due to a buried sphere used as a magnetic dipole calculated across a N–S profile.
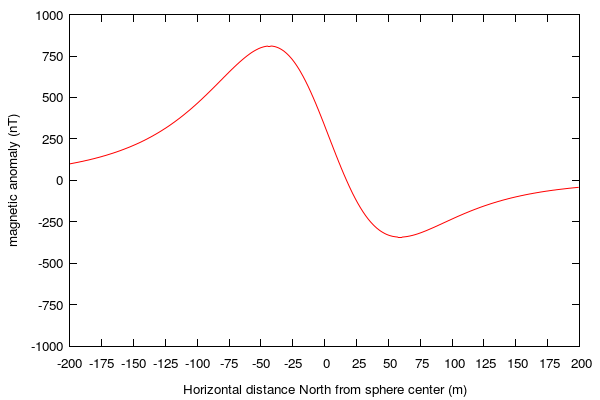
The gnuplot script requires a data file named dipole.dat which is made from the output of the perl script dipole.pl.
# USAGE:
# on the command line type:
# gnuplot dipole.gnu
reset
set terminal pngcairo enhanced font "arial,10" fontscale 1.0 size 600,400
set output 'mag_anomaly.png'
# Axes label
set xlabel 'Horizontal distance North from sphere center (m)'
set ylabel 'magnetic anomaly (nT)'
# Axes ranges
set xrange [-200:200]
set yrange [-1000:1000]
# Axes tics
set xtics 25
set ytics 250
set style fill transparent solid 0.15
# set key Left
plot "dipole.dat" using 1:2 with line lt rgb "red" notitle
Draw the model geometry with LaTeX and TikZ
The following LaTeX and TikZ code draws the figure of the model geometry presented at the top of the page.
\documentclass[tikz, border = 1mm]{standalone}
\usepackage{tikz,tikz-3dplot}
\begin{document}
\tdplotsetmaincoords{60}{110}
\pgfmathsetmacro{\rvec}{.8}
\pgfmathsetmacro{\thetavec}{30}
\pgfmathsetmacro{\phivec}{60}
\pgfmathsetmacro{\loopvec}{360}
\begin{tikzpicture}[scale=5,tdplot_main_coords]
\coordinate (O) at (0,0,0);
\tdplottransformmainscreen{0}{0}{0}
\shade[tdplot_screen_coords, ball color = red!20] (\tdplotresx,\tdplotresy) circle (0.35);
\draw[thick,->] (0,0,0) -- (1,0,0) node[anchor=north east]{$y, East$};
\draw[thick,->] (0,0,0) -- (0,1,0) node[anchor=north east]{$x, North$};
\draw[very thick,->] (0,0,0) -- (0,0,-1) node[anchor=north]{$z, down$};
\draw [dashed] (0.75,-0.5,0.9) -- node[anchor=south east]{$r_z$}(0.75,-0.5,0);
\draw [dashed] (0.75,0,00) -- node[anchor=north]{$r_y$}(0.75,-0.5,0);
\draw [dashed] (0,-0.5,0) -- node[anchor=north west]{$r_x$}(0.75,-0.5,0);
\draw [dashed] (0.75,-0.5,0.9) -- node[anchor=north]{$r$}(0,0,0);
\draw[dashed, -stealth] (O) -- node[above] {$a$} (0,0.3,0.3);
\draw[very thick, red, -stealth] (0,-0.25, 0.25) -- (0,0.25, -.25) node[anchor=north west]{$\vec \mu$};
\tdplottransformmainscreen{0.75}{-0.5}{0.9}
\draw[teal!20, line width = 6] (0,-1.0,0.5) -- (0,1.0,0.5)
node [teal, anchor=north] {surface};
\shade[tdplot_screen_coords, ball color = black!20] (\tdplotresx,\tdplotresy) circle (0.015) ;
\node at (0.75,-0.5,0.95) {$P$};
\node at (0.05,0.05,0) {$O$};
\end{tikzpicture}
\end{document}
Some References
- Telford, W.M., Geldart, L.P. and Sheriff, R.E. (1990) Applied Geophysics, Cambridge University Press.
- Blakely, R.J., 1996. Potential Theory in Gravity and Magnetic Applications. Cambridge University Press.