Magnetic anomaly due to a prism
calculate the magnetic anomaly due to one or more buried vertical-sided prisms
Contents
Introduction
Code is provided to calculate the magnetic anomaly due to a vertical-sided prism with horizontal top and bottom and uniform magnetization. The prism can be rotated about a vertical axis with respect to geographic north. This code can be used to model magnetic anomalies from geologic features that can be represented by prisms, such as vertical dikes or horizontal beds, and can be used to build more complex models using multiple prisms.
The following canvas illustrates the calculation of a magnetic anomaly due to a buried prism, like a lava flow or igneous sill. The prism is assumed to extend in and out of the screen by 1000 m. Use the mouse to change the depth of the prism and use the slider bar to change the inclination of the magnetic field.
Mathematical Model
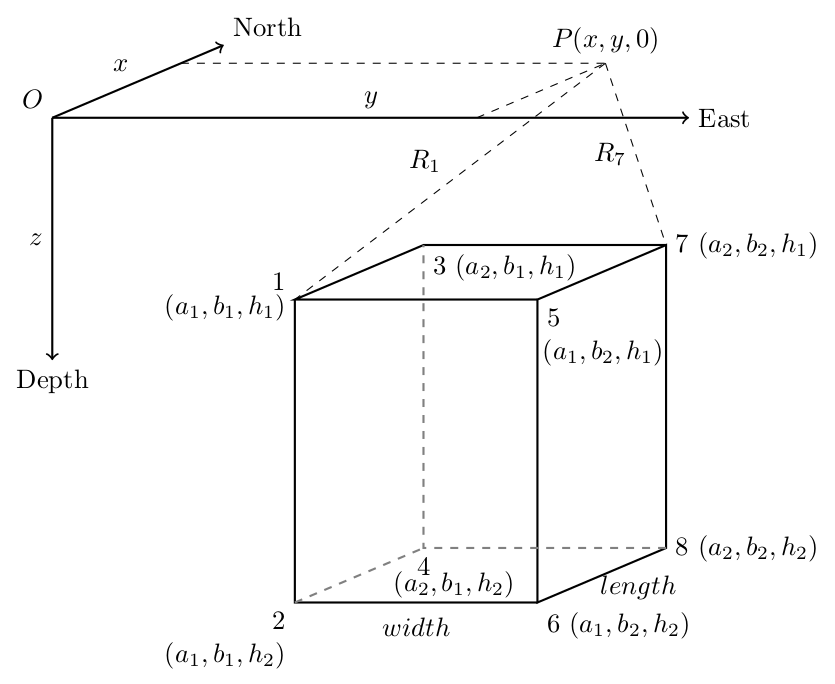
The following equations are used in calculating the magnetic anomaly due to a vertical sided prism. Please refer to the paper by, Rao & Babu (1991).
The main equation: \begin{align} \Delta T(x,y,0) & = G_1 \ln F_1 + G_2 \ln F_2 + G_3 \ln F_3+ G_4 F_4 + G_5 F_5 \end{align} where, \begin{align} F_1 & = \frac{(R_2 + \alpha_1)(R_3 + \alpha_2)(R_5 + \alpha_1)(R_8 + \alpha_2)}{(R_1 + \alpha_1)(R_4 + \alpha_2)(R_6 + \alpha_1)(R_7 + \alpha_2)}\\ F_2 & = \frac{(R_2 + \beta_1)(R_3 + \beta_1)(R_5 + \beta_2)(R_8 + \beta_2)}{(R_1 + \beta_1)(R_4 + \beta_1)(R_6 + \beta_2)(R_7 + \beta_2)}\\ F_3 & = \frac{(R_2 + h_2)(R_3 + h_1)(R_5 + h_1)(R_8 + h_2)}{(R_1 + h_1)(R_4 + h_2)(R_6 + h_2)(R_7 + h_1)} \end{align} \begin{align} F_4 & = \tan^{-1}\frac{\alpha_2 h_2}{R_8 \beta_2} - \tan^{-1}\frac{\alpha_1 h_2}{R_6 \beta_2} - \tan^{-1}\frac{\alpha_2 h_2}{R_4 \beta_1} + \tan^{-1}\frac{\alpha_1 h_2}{R_2 \beta_1} - \tan^{-1}\frac{\alpha_2 h_1}{R_7 \beta_2} + \tan^{-1}\frac{\alpha_1 h_1}{R_5 \beta_2} + \tan^{-1}\frac{\alpha_2 h_1}{R_3 \beta_1} - \tan^{-1}\frac{\alpha_1 h_1}{R_1 \beta_1}\\ F_5 & = \tan^{-1}\frac{\beta_2 h_2}{R_8 \alpha_2} - \tan^{-1}\frac{\beta_2 h_2}{R_6 \alpha_1} - \tan^{-1}\frac{\beta_1 h_2}{R_4 \alpha_2} + \tan^{-1}\frac{\beta_1 h_2}{R_2 \alpha_1} - \tan^{-1}\frac{\beta_2 h_1}{R_7 \alpha_2} + \tan^{-1}\frac{\beta_2 h_1}{R_5 \alpha_1} + \tan^{-1}\frac{\beta_1 h_1}{R_3 \alpha_2} - \tan^{-1}\frac{\beta_1 h_1}{R_1 \alpha_1} \end{align} with, \begin{align} R_1 & = \sqrt{\alpha_1^2+\beta_1^2+h_1^2}\\ R_2 & = \sqrt{\alpha_1^2 + \beta_1^2 + h_2^2}\\ R_3 & = \sqrt{\alpha_2^2 + \beta_1^2 + h_1^2}\\ R_4 & = \sqrt{\alpha_2^2 + \beta_1^2 + h_2^2}\\ R_5 & = \sqrt{\alpha_1^2+\beta_2^2+h_1^2}\\ R_6 & = \sqrt{\alpha_1^2 + \beta_2^2 + h_2^2}\\ R_7 & = \sqrt{\alpha_2^2 + \beta_2^2 + h_1^2}\\ R_8 & = \sqrt{\alpha_2^2 + \beta_2^2 + h_2^2}\\ \end{align} and, \begin{align} \alpha_1 & = a_1 - x'\\ \alpha_2 & = a_2 - x'\\ \beta_1 & = b_1 - y'\\ \beta_2 & = b_2 - y'\\ G_1 & = EI(Mr+Nq)\\ G_2 & = EI(Lr+Np)\\ G_3 & = EI(Lq+Mp)\\ G_4 & = EI(Nr-Mq)\\ G_5 & = EI(Nr - Lp)\\ x' & = x \cos \theta + y \sin \theta\\ y' & = -x \sin \theta + y \cos \theta\\ p & = \cos I \cos(D-\theta)\\ q & = \cos I \sin(D-\theta)\\ r & = \sin I\\ L & = \cos I_o \cos(D_o-\theta)\\ M & = \cos I_o \sin(D_o-\theta)\\ N & = \sin I_o \end{align}
Model assumptions
This model assumes that:PERL Codes
Identify cube
PERL script, ''create_grid.pl'', generates an ascii (text) file in X Y format that represents a box. The box will be centered at grid location 0,0 and extend 500 units in each cardinal direction. This grid file is used by the PERL script, ''magcube.pl'', as input. Box values can be adjusted by changing the values for ''$rmin'', ''$rmax'', ''$cmin'', ''$cmax''. Script, ''create_grid.pl'', is executed on the command line.
$rmin = -500;
$rmax = 500;
$cmin = -500;
$cmax = 500;
for (my $row = $rmin; $row <= $rmax; $row+= 20) {
for (my $col = $cmin; $col <= $cmax; $col+= 20) {
print "$col $row\n";
}
}
Configure magnetic properties
This file, ''magcube.conf'', contains the input values required by the PERL script, ''magcube.pl (see below)''. The format is KEYWORD=value. Only values can be modified; the KEYWORDS should NOT be changed. This configuration file should be co-located with the ''magcube.pl'' script.
###################################
# Configuration file for magcube.pl
###################################
INPUT_GRIDFILE=grid_-500_500_-500_500.xy
OUTPUT_GRIDFILE=mag_anomaly.out
#
# A value for the center of the prism
CENTER_EAST=0
CENTER_NORTH=0
#
# Length of the prism in the x-direction (units = meters)
###################################
EAST_LENGTH=1
#
#Length in the y-direction (units = meters)
NORTH_LENGTH=1000
#
# Assume the ground surface is 0 meters and down is a positive direction of measurement (units = meters)
SURFACE_TO_TOP=50
SURFACE_TO_BOTTOM=2000
#
# Theta is the angle from North (units = degrees)
THETA=-30
#
# The inclination and declination of the Earth's magnetic field (units = degrees)
INC_EARTH_MAG_FIELD=45
DEC_EARTH_MAG_FIELD=.0001
#
# The inclination and declination of the vector of magnetization (units = degrees)
INC_VECTOR_OF_MAG=45
DEC_VECTOR_OF_MAG=.0001
#
# The intensity of magnetization (unis = nT)
INTENSITY=400
#
# Map grid spacing (units = meters)
GRID_SPACING=20
Calculate magnetic field
PERL script, ''magcube.pl'', calculates the magnetic anomaly due to a buried cube as specified by parameters in the configuration file, ''magcube.conf''. Script, ''magcube.pl'', is executed on the command line.
##############################
# Program: mag_cube_radians.pl
# Authors: Chuck and Laura Connor
# Date: (original: October, 2001) This version: January, 2014
# Language: PERL
#
# Purpose: This program calculates the magnetic field due
# to a set of vertical -sided prisms using the algorithm of
# Rao and Babu (1991, Geophysics).
# Input files:
# magcube.conf (Specifically, this file contains the prism geometry and magnetic properties
# grid file (ASCII file in X Y format of grid locations of box; name specified by the user)
#
# Output to STDOUT:
# X Y Z - the x,y, point location and total magnetic field.
###############################
use strict;
use warnings;
use Math::Trig;
use constant PI => 4 * atan2(1, 1);
# Degrees to radians conversion factor
use constant DEG2RAD => 0.017453293;
my $args = @ARGV;
my %Param;
my $conf = "mag_cube.conf";
open CONF, "< $conf" or die "Can't open $conf : $!";
while() {
if (/^$/ or /^#/) { next; }
(my $key, my $value) = split "=",$_;
chomp($value);
$Param{$key} = $value;
print STDERR "$key=$Param{$key}\n";
}
open IN, "< $Param{INPUT_GRIDFILE}" or die "Unable to open $Param{INPUT_GRIDFILE}: [$!]";
open OUT, "> $Param{OUTPUT_GRIDFILE}" or die "Unable to open $Param{OUTPUT_GRIDFILE}: [$!]";
my @lines = ;
my $max = -1e9;
my $min = 1e9;
foreach my $line (@lines) {
if ($line =~ m/^#/ ) {next;}
(my $east, my $north) = split(" ", $line);
#print STDERR "$east, $north ";
my $mf = calculate($east, $north, \\%Param);
if ($mf > $max) {$max = $mf;}
if ($mf < $min) {$min = $mf;}
print OUT "$east $north $mf\\n";
}
print STDERR "Min: $min nT, Max: $max nT\n";
`perl plot_2D_anomaly.gmt.pl $min $max $Param{GRID_SPACING} $Param{CENTER_EAST} $Param{CENTER_NORTH} $Param{OUTPUT_GRIDFILE}`;
print STDERR "Finished!\n";
sub calculate {
my $P_ref = $_[2];
my $easting = $_[0];
my $northing = $_[1];
#print STDERR "POINT: $easting, $northing\n";
my $em_inc = DEG2RAD * $$P_ref{INC_EARTH_MAG_FIELD};
#print STDERR "Inclination of Earth's Magnetic Field: $em_inc\n";
my $em_dec = DEG2RAD * $$P_ref{DEC_EARTH_MAG_FIELD};
#print STDERR "Declination of Earth's Magnetic Field: $em_dec\n";
my $theta = DEG2RAD * $$P_ref{THETA};
#print STDERR "Theta: $theta\n";
my $intensity = $$P_ref{INTENSITY};
#print STDERR "Intensity: $intensity\n";
my $vm_inc = DEG2RAD * $$P_ref{INC_VECTOR_OF_MAG};
#print STDERR "Inclination of the vector of magnetization: $vm_inc\n";
my $vm_dec = DEG2RAD * $$P_ref{DEC_VECTOR_OF_MAG};
#print STDERR "Declination of the vector of magnetization: $vm_dec\n";
my $half_east_length = $$P_ref{EAST_LENGTH} / 2 + .00001;
my $half_north_length = $$P_ref{NORTH_LENGTH} / 2 + .00001;
my $west = $$P_ref{CENTER_EAST} - $half_east_length;
my $east = $$P_ref{CENTER_EAST} + $half_east_length;
my $south = $$P_ref{CENTER_NORTH} - $half_north_length;
my $north = $$P_ref{CENTER_NORTH} + $half_north_length;
#print STDERR "a1 a2 b1 b2: ($a1, $a2, $b1, $b2)\n";
my $h1 = $$P_ref{SURFACE_TO_TOP} + .00001;
#print STDERR "Surface to Top = $h1\n";
my $h2 = $$P_ref{SURFACE_TO_BOTTOM} +.00001;
#print STDERR "Surface to Bottom = $h2\n";
# Calculate the earth's inclination and declination w.r.t. theta
my $p = cos( $em_inc) * cos( $em_dec - $theta);
my $q = cos($em_inc) * sin($em_dec - $theta);
my $r = sin($em_inc);
#print STDERR "p q r: ($p, $q, $r)\n";
# Calculate the vector of magnetization's inclination and declination wrt theta
my $L = cos($vm_inc) * cos($vm_dec - $theta);
my $M = cos($vm_inc) * sin($vm_dec - $theta);
my $N = sin($vm_inc);
#print STDERR "L M N: ($L, $M, $N)\n";
# Calculate amplitudes of the resulting magnetic field
my $g1 = $intensity * ($M * $r + $N * $q);
my $g2 = $intensity * ($L * $r + $N * $p);
my $g3 = $intensity * ($L * $q + $M * $p);
my $g4 = $intensity * ($N * $r - $M * $q);
my $g5 = $intensity * ($N * $r - $L* $p);
#print STDERR "Amplitudes: ($g1, $g2, $g3, $g4, $g5)\n";
# Rotate the coordinate system w.r.t. theta
#my $newy = $yp - $$P_ref{CENTER_Y};
#my $newx = $xp - $$P_ref{CENTER_X};
#my $xpr = $yp * cos($theta) + $xp * sin($theta);
#my $ypr = -$xp * sin($theta) + $yp * cos($theta);
#my $ypr = $xp * cos($theta) - $yp * sin($theta);
#print STDERR "$xp, $yp (0, 0)= $xpr, $ypr\n";
# sin(0) = 0; cos(0) = 1; sin(90) = 1 cos(90) 0
my $xp = $easting * cos($theta) - $northing * sin($theta);
my $yp = $easting * sin($theta) + $northing * cos($theta);
# Distance between the
my $ap1 = $south - $yp;
my $ap2 = $north - $yp;
my $bp1 = $west - $xp;
my $bp2 = $east - $xp;
#print STDERR "ap1 ap2 bp1 bp2: ($ap1, $ap2, $bp1, $bp2)\n";
# Find the relative distances
my $ap1_ap1 = $ap1 * $ap1; my $bp1_bp1 = $bp1 * $bp1; my $h1_h1 = $h1 * $h1;
my $ap2_ap2 = $ap2 * $ap2; my $bp2_bp2 = $bp2 * $bp2; my $h2_h2 = $h2 * $h2;
my $r1 = sqrt($ap1_ap1 + $bp1_bp1 + $h1_h1);
my $r2 = sqrt($ap1_ap1 + $bp1_bp1 + $h2_h2);
my $r3 = sqrt($ap2_ap2 + $bp1_bp1 + $h1_h1);
my $r4 = sqrt($ap2_ap2 + $bp1_bp1 + $h2_h2);
my $r5 = sqrt($ap1_ap1 + $bp2_bp2 + $h1_h1);
my $r6 = sqrt($ap1_ap1 + $bp2_bp2 + $h2_h2);
my $r7 = sqrt($ap2_ap2 + $bp2_bp2 + $h1_h1);
my $r8 = sqrt($ap2_ap2 + $bp2_bp2 + $h2_h2);
#print STDERR "r1 r2 r3 r4 r5 r6 r7 r8\n", ($r1, $r2, $r3, $r4, $r5, $r6, $r7, $r8);
# do the trig!
my $f1 = ($r2 + $ap1) * ($r3 + $ap2) * ($r5 + $ap1) * ($r8 + $ap2) / (($r1 + $ap1) * ($r4 + $ap2) * ($r6 + $ap1) * ($r7 + $ap2));
my $f2 = ($r2 + $bp1) * ($r3 + $bp1) * ($r5 + $bp2) * ($r8 + $bp2) / (($r1 + $bp1) * ($r4 + $bp1) * ($r6 + $bp2) * ($r7 + $bp2));
my $f3 = ($r2 + $h2) * ($r3 + $h1) * ($r5 + $h1) * ($r8 + $h2) / (($r1 + $h1) * ($r4 + $h2) * ($r6 + $h2) * ($r7 + $h1));
my $f4 = atan($ap2 * $h2 / ($r8 * $bp2)) - atan($ap1 * $h2 / ($r6 * $bp2))
- atan($ap2 * $h2 / ($r4 * $bp1)) + atan($ap1 * $h2 / ($r2 * $bp1))
- atan($ap2 * $h1 / ($r7 * $bp2)) + atan($ap1 * $h1 /($r5*$bp2))
+ atan($ap2 * $h1 / ($r3 * $bp1)) - atan($ap1 * $h1 / ($r1 * $bp1));
my $f5 = atan($bp2 * $h2 / ($r8 * $ap2)) - atan($bp2 * $h2 / ($r6 * $ap1))
- atan($bp1 * $h2 / ($r4 * $ap2)) + atan($bp1 * $h2 / ($r2 * $ap1))
- atan($bp2 * $h1 / ($r7 * $ap2)) + atan($bp2 * $h1 / ($r5 * $ap1))
+ atan($bp1 * $h1 / ($r3 * $ap2)) - atan($bp1 * $h1 / ($r1 * $ap1));
#print STDERR "f1 f2 f3 f4 f5: ($f1, $f2, $f3, $f4, $f5)\n";
#calcuate the magnetic field at x,y using these terms
my $T = $g1 * log($f1) + $g2 * log($f2) + $g3 * log($f3) + $g4 * ($f4) + $g5 * ($f5);
return $T;
}
Plot magnetic anomaly
PERL script, ''plot2D_anomaly.gmt.pl'', uses Generic Mapping Tools(GMT) to plot the resulting magnetic anomaly due to a buried cube as calculated by the script ''magcube.pl''. This script requires the installation of GMT version 5. Note: the gmt commands are listed in blue. The GMT commands can also be run from the command line with actual values substituted for the PERL variables.
#! /usr/bin/perl
$in = "$ARGV[5]";
$out = "plot_2D.eps";
$min = $ARGV[0];
$max = $ARGV[1];
$gs = $ARGV[2];
`gmt surface -I$gs $in -G$in.grd \`gmtinfo -I2 $in \` -V`;
`gmt makecpt -Chaxby -T$min/$max/1 -V > mag.cpt`;
`gmt grdimage --FONT_TITLE=8p --FONT_LABEL=8p --FONT_ANNOT_PRIMARY=8p $in.grd -X1i -Y2i -R -JX6i -Cmag.cpt -P -E100 -V -K> $out`;
`gmt grdcontour $in.grd -R -JX -C10 -Bxaf100+l"Easting"+u"m" -Byaf100+l"Northing"+u"m" -BSnWe -W0.25p,0 -O -K >> $out`;
`gmt psxy -R -JX -SC0.1i -G0 -V -K -O <> $out
$ARGV[3] $ARGV[4]
EOF
`;
$cint = int(($max - $min)/10);
$scale_anot_int = $cint*2;
$scale_str = "a"."$scale_anot_int";
`gmt psscale --FONT_TITLE=8p --FONT_LABEL=8p --FONT_ANNOT_PRIMARY=8p -D3i/-0.8i/4i/0.1ih -Cmag.cpt -B$scale_str/:'nT': -O -V >> $out`;
`gmt ps2raster $out -A -Tg -V`;
`rm *.grd *.cpt ;`
Code for example implemented in P5.js
The p5.js code for the interactive simulation above:
magcube.jsSome References
- Telford, W.M., Telford, W.M., Geldart, L.P., Sheriff, R.E. and Sheriff, R.E. (1990) Applied Geophysics. Cambridge University Press.
- Rao, D. Bhaskara, and N. Ramesh Babu (1991) A rapid method for three-dimensional modeling of magnetic anomalies. Geophysics (56)11:1729–1737. doi: 10.1190/1.1442985