Introduction to inversion

Learn about inversion using the magnetic anomaly of a sphere using a two-step adaptive learning search find depth

Contents

Introduction

We are going to continue using the noisy magnetic sphere anomaly to test drive inversion methods. We are inverting on one parameter - depth to the center of the buried sphere.

In this example, the forward solution is the magnetic anomaly due to a buried sphere. A description of the forward model is available here.

The methd used here is a two-step method. First, we do a coarse inversion using a brute force search. This produces a best-fit RMSE value. Next, we search around this approximate answer using a gradient search method. When we are near the RMSE minimum, the gradient search does a good (and reasonably fast) job of finding the best-fit depth.

[Top]

Structure of the Inversion

The basic structure of this inversion is illustrated in the flowchart. Two bits of information are needed:

  • The input data file consists of the x,y, coordinates of the magnetic observations, the observed magnetic value, and, initially, a column of zeros, representing the calculated magnetic anomaly.
  • The initial geometry of the sphere. All parameters are set in this input. Only one parameter (depth in this case) will be adjusted. Note that the sphere parameters are specified in the main () function in the source code in this example.

With these inputs the main() code calls the function to perform the coarse search. The coarse search is simply a brute force calculation to find the minimum RMSE. In this case ten values are found. The depth corresponding to the minimum RMSE resulting from the coasre search is passed to the gradient function. The gradient function then searches a narrow range of depth values to find the optimal value.

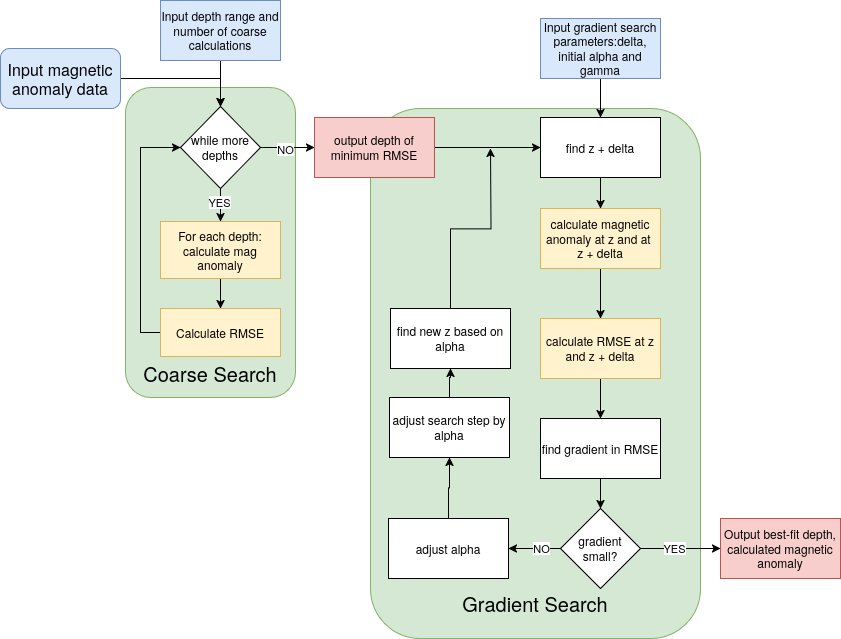
adaptiveflowchart
[Top]

The Gradient Search Function

Sevral parameters are specified to run this gradient search algorithm. delta specifies the small step taken to determine the local gradient. For exampe, if delta = 1, the depth of the sphere center is changed by one meter to calculate the local gradient. The parameters alpha and gamma have a lot in common with the "temeprature" in simulated annealing. The alpha parameter governs how fast the sphere depth is changed in successive calculations. The gamma parameter controls how fast alpha decays as the RMSE values of successive calculations converge. The algorithm stops if there is no change in RMSE within some tolerance or a maxmimum number of iterations is reached.

[Top]

The C code

You need five files to compile and run this code:

Download these files (all in the same directory). To compile the code, on the command line type: make

To run the code type: ./adaptive mag_sphere.dat > outputfilename.dat

If all goes well, the first lines of your output file should look like:


row count read from input file 2000
sphere1.z at end of coarse search = 333.400000
Optimized depth: 297.906206
-1000.000000 0.000000 -5.490345 6.120217
-999.000000 0.000000 11.391087 6.140306
-998.000000 0.000000 9.652076 6.160478
-997.000000 0.000000 10.416932 6.180734
-996.000000 0.000000 -31.523155 6.201074

Note that at the end of the coasre search the depth is estimated to be about 333 m. This depth is refined by the gradient search to be about 298 m. The final depth estimate is very close to the "real" depth of 300 m used to create the input file.

[Top]

Things to Try

  • Make sure you can download, compile and run the code. Plot up the output to compare the observed and calculated magnetic anomalies.
  • Experiment with changing the search parameters. What happens if the coarse search does not include the optimal region? Change the adaptive search parameters: delta, gamma, and alpha_init
  • Try modifying the code to invert for a different parameter, like the magnitude of the vector of magnetization of the buried sphere. Note that you will have to make changes in the golden search function and in the main function.
  • In the current version of the code, the sphere parameters are specified in main(). Try modifying the code so these parameters are read from a configuration file. Hint: see the C shortcourse for an example of reading a configuration file: data4.c