Gravity Anomaly Over a Sedimentary Basin

Use Bott's method to model gravity data measured across a sedimentary basin

Mathematical model
Model assumptions
Calculating the model using perl
Plotting the output with gnuplot
References and citation

Introduction

Bott proposed an iterative method for finding the variation in thickness of sediments within a sedimentary basin, using a profile of gravity measurements collected across the basin. He used a 2D approximation of the basin (no variation in thickness along the length of the basin). The method relies on an iterative approach. First, the Bouguer slab formula is used to guess basin depth based on each gravity point along the profile. Second, a forward model (gbox) is calculated using these approximate thicknesses and the sum of the gravity anomalies due to these vertical-sided prisms. Third, thickness is re-estimated using the Bouguer slab formula. These steps are repeated until there is very small changes in thickness between iterations.

M. Bott's method works because the gravity stations are close to the top of the sedimentary basin (literally on it!). This means that the Bouguer slab approximation to the gravity anomaly works well. If the top of the sedimentary basin were deeper, the Bouguer assumption starts to lose accuracy. Bott's method can be used for other structures (calderas, exposed igneous intrusions, lunar craters) as long as the body crops out at the surface.

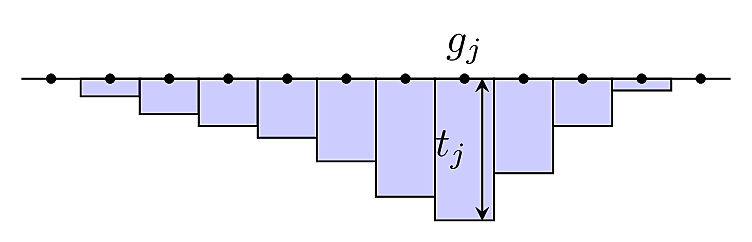
Below, a 2D sedimentary basin divided into $N$ blocks. Each block has one gravity observation, $g_j$, and one thickness, $t_j$.

[Top]

Mathematical model and Bott's iterative method

Step 1:

Assume there is one gravity reading for each block of thickness $t_j$ along a profile across a sedimentary basin.

Step 2:

Calculate the expected gravity anomaly assuming that the thickness at each point is related to the thickness of an infinite Bouguer slab $$t_j^{(1)} = \frac{g_j}{2 \pi G \Delta \rho} \textrm{, } j = 1, 2,\textrm{ ..., }N $$ where,

$t_j$ is the thickness of block $j$, the superscript $(1)$ means this is the value of thickness on the first iteration.
$\Delta \rho$ is the density contrast between the basin and the surrounding rock.
$g_j$ is the measured gravity anomaly in block $j$
$G$ is the gravitational constant
There are a total of $N$ blocks

Step 3:

For each block, using the gbox routine, calculate the gravity anomaly at point $g_j$ due to all the prisms of density contrast $\Delta \rho$ and thicknesses $t_j$.

Step 4:

for each block, calculate the difference between the observed gravity, $g_j$ and the calculated gravity, $g_j^{(1)}$ $$\Delta g_j = g_j - g_j^{(1)}$$

Step 5:

For each block, calculate the new thickness using $\Delta g_j$ and the infinite slab formula $$t_j^{(2)} = \frac{\Delta g_j}{2 \pi G \Delta \rho} + t_j^{(1)}$$ The superscript $(2)$ indicates this is the next iterative solution to thickness.

Step 6:

Repeat steps 3--5 until for each block $$t_j^{n} \approx t_j^{n-1}$$

[Top]

Model assumptions

The bott model assumes:

The basin is 2D with no variation in the basin along its strike (the long axis of the basin).
The basin is characterized by a single density contrast with the surrounding rocks.
There are no other sources of gravity anomalies.
The gravity data are detrended and shifted so that the gravity anomaly on the margins of the basin approach zero on both sides.

[Top]

Calculate the gravity using perl

A solution for determining the thickness of a sedimentary basin using M. Bott's method is listed below. This perl script uses a function to calculate the Bouguer slab gravity anomaly and a function to calculate the gravity anomaly due to a vertical-sided prism (gbox model).

This script requires an input file of gravity data and assumes that detrended and interpolated gravity anomaly values are spaced at 500 m intervals along a profile. An example input file example_gravity_line.dat is provided.

Input file: example_gravity_line.dat


distance (m)     gravity (mGal)

500 -5.90558521025545
1000 -3.9420587574959
1500 -3.60792947653623
2000 -3.63613631638196
2500 -2.56108510666886
3000 -1.8207895293818
3500 -0.640688786133412
4000 -0.0434827309838897
4500 -0.0222051924368438
5000 -0.737114482460122
5500 -1.4520237724834
6000 -2.29359599522139
6500 -4.66777361454465
7000 -7.04195123386791
7500 -7.16812176086817
8000 -8.63533442734315
8500 -12.3984916183681
9000 -16.161648809393
9500 -19.6245539312066
10000 -21.9915146434067
10500 -24.3584753556068
11000 -26.725436067807
11500 -29.1371138801307
12000 -31.5076851550556
12500 -31.1403033856382
13000 -30.634562817686
13500 -29.3579612008566
14000 -28.2628543131522
14500 -27.6912600182527
15000 -27.1196657233532
15500 -26.4488499644341
16000 -25.3859450612425
16500 -23.5052774319269
17000 -21.6246098026112
17500 -19.7439421732956
18000 -18.2039449878781
18500 -16.7816409844282
19000 -15.474531712738
19500 -14.3643439372883
20000 -13.277647238518
20500 -12.2667150710887
21000 -11.1312705806165
21500 -9.50306530310009
22000 -6.897276610137
22500 -4.29148791717391
23000 -1.92982633962782
23500 -0.905302319995194
24000 -0.137586632295369
24500 0.0439502418050779

perl script: bott.pl


# Invert gravity data to calculate the 2D
# thickness of sediments (uniform density contrast) within a 
# sedimentary basin, using the algorithm of M. Bott.

#input: file of detrended gravity values (2 columns)
#         1. anomaly should -> 0 at each end of the profile
#         2. interpolated and detrended gravity -> this code
#            assumes gravity data are spaced at 500 m intervals 
#            along the profile line
#         3. input file is in profile distance (m) and gravity (mgal)
#
#first lines of the input file look like:
#        500 -5.90558521025545
#        1000 -3.9420587574959
#
# change the density, $rho in the main part of the code
# likely no other alterations are needed for a given run.
# 
#output:
#  First column: distance along profile line (m, same as input))
#  Second column: thickness of the basin at that point (m)
#  Third column: observed gravity at that point (mgal, same as input)
#  Fourth column: calculated gravity at that point (mgal)
#
#coded up by C. Connor, June, 2020


sub gbox($$$$$$$$$$) { 
 
 #   Function gbox computes the vertical attraction of a 
 #   rectangular prism.  Sides of prism are parallel to x,y,z axes,
 #   and z axis is vertical down.  
 #   
 #   Input parameters:
 #   Observation point is (x0,y0,z0).  The prism extends from x1 (west)
 #   to x2(east), from y1(south) to y2(north), and from z1(depth to top)  
 #   to z2(depth to bottom) 
 #   in the x, y, and z directions, respectively. 
#
#    Distance units in meters. 
#    x is positive east
#    y is positive north
#    z is positive down
#
#    Density of prism is rho. This is the density contrast between
#    the prism and surrounding rock.  rho in units of kg/(m**3). 
#    
#    Output parameters:
#    Vertical attraction of gravity, g, in mGal. 
#
#
#    Modified from Blakely, 1997, subroutine B.6
#    Translated to PERL by C. Connor

#observation point
$x0 = shift;
$y0 = shift;
$z0 = shift;
$x1 = shift;
$y1 = shift;
$z1 = shift;
$x2 = shift;
$y2 = shift;
$z2 = shift;
$rho = shift;

my $small = 1e-10;
my $gamma = 6.670e-11;
my $twopi = 6.2831853;
my $si2mg = 1.0e5;
my $g_temp = $gamma * $si2mg;
  
  $xs[0] = $x0 - $x1;
  $ys[0] = $y0 - $y1;
  $zs[0] = $z0 - $z1;
  $xs[1] = $x0 - $x2;
  $ys[1] = $y0 - $y2;
  $zs[1] = $z0 - $z2;
  $isign[0] = -1.0;
  $isign[1] = 1.0;
  
  $sum=0.0;
  for ($x=0; $x<2; $x++) {
    for ($y=0; $y<2; $y++) {
      for ($z=0; $z<2; $z++) {
         $rijk = sqrt($xs[$x]*$xs[$x] + $ys[$y]*$ys[$y] + $zs[$z]*$zs[$z]);
	       $ijk = $isign[$x]*$isign[$y]*$isign[$z];
	       $arg1 = atan2(($xs[$x]*$ys[$y]),($zs[$z]*$rijk));
	       if ($arg1 < 0.0) {$arg1 = $arg1 + $twopi};
	       $arg2 = $rijk+$ys[$y];
	       $arg3 = $rijk+$xs[$x];
	       if ($arg2 <= 0.0) { $arg2 = $small};
	       if ($arg3 <= 0.0) {$arg3 = $small};
	       $arg2 = log($arg2);
	       $arg3 = log($arg3);
	       $sum += $ijk*($zs[$z]*$arg1-$xs[$x]*$arg2-$ys[$y]*$arg3);
      }
    }
  }
  $g = $rho * $sum * $g_temp;
  return $g;
}

#############################################
# calculate the thickness from 
# simple Bouguer gravity anomaly 
# for an assumed value of density contrast
#############################################
sub bouguer($$) {

 my $point_gravity = shift; #mgal
 my $rho = shift; #kg/m3
 my $pi = 3.14159;
 my $bigG  = 6.670e-11;
 $point_gravity = $point_gravity/1e5;
 $thickness = $point_gravity/(2*$pi*$bigG*$rho);
 return $thickness; #meters
};

###Main Program ####
#x0 is distance of interpolated gravity station along line
$y0 = 0;  #gravity station on profile
$z0 = 0; #gravity station at surface

$spacing = 500; #regular spacing between obs. (m)
$y1 = -5000; #long length of prism (m)
$y2 = 5000;
$rho = -500; #density contrast (kg/m3)

open (IN, "<$ARGV[0]") || die ("Cannot open $ARGV[0]: $!");

$i = 0;
@MyPointsDATA = ;

foreach $line (@MyPointsDATA) {
  ($x0[$i], $obs_gravity[$i]) = split " ", $line;
  if ($obs_gravity[$i] < 0) {
    $thick[$i] = bouguer($obs_gravity[$i], $rho);
  } else {
    $thick[$i] = 0;
  }
  $i++;
}
$n = $i;

# Note: in this simplified version
#      the counters $i and $j are the same
# create prism file
for ($j = 0; $j < $n; $j++) {
  $prism[$j][0] = $x0[$j] - $spacing/2;
  $prism[$j][1] = $y1;
  $prism[$j][2] = 0.1;
  $prism[$j][3] = $x0[$j] + $spacing/2;
  $prism[$j][4] = $y2;
  $prism[$j][5] = $thick[$j];
  $prism[$j][6] = $rho;
};

# iterate 10 x
# to get convergence between
# obs and calculated
for($t = 0; $t < 10; $t++) {
  #for each point on the profile
  for ($i = 0; $i < $n; $i++) {
    #initialize the gravity value
    $calc_gravity[$i] = 0;
    $prism[$i][5] = $thick[$i];
    #for each prism
    for($j = 0; $j < $n; $j++) {
      #calculate the gravity 
      #summing for each prism 
      $calc_gravity[$i] += 
        gbox($x0[$i],
             $y0,
             $z0,
             $prism[$j][0],
             $prism[$j][1],
             $prism[$j][2],
             $prism[$j][3],
             $prism[$j][4],
             $prism[$j][5],
             $prism[$j][6] );
      };  
   
      #find the discrepency between calculated and observed
      $diff_gravity[$i] = $obs_gravity[$i] - $calc_gravity[$i];

      # Use the simple Bouguer formula
      # to calculate the change in thickness needed
      # to account for the gravity discrepency
      $del_t = bouguer($diff_gravity[$i], $rho);

      # Adjust the thickness for the next iteration
      $thick[$i] += $del_t; 

      # Do not allow negative basin thicknesses
      if ($thick[$i] < 0){$thick[$i] = 0;};
  };
};

# All done, print the results
for ($i=0; $i<$n; $i++){
  print("$x0[$i] $thick[$i] $obs_gravity[$i] $calc_gravity[$i] \n");
};

To execute this perl script from the command line, type:


perl bott.pl example_gravity_line.dat > profile1-bott.dat

The script creates an output file profile1-bott.dat


profile-position (m) basin-thickness (m) observed-gravity (mGal) calculated-gravity (mGal)

500 451.547814419572 -5.90558521025545 -5.8591070903909 
1000 133.734467278076 -3.9420587574959 -3.96347742639325 
1500 153.827513485608 -3.60792947653623 -3.61295325018673 
2000 173.764074664439 -3.63613631638196 -3.64089026536985 
2500 98.7591619462124 -2.56108510666886 -2.56479467935169 
3000 63.185963455787 -1.8207895293818 -1.82450850510974 
3500 2.63568428721334 -0.640688786133412 -0.644262205545986 
4000 0 -0.0434827309838897 -0.613752725184319 
4500 0 -0.0222051924368438 -0.711670764250035 
5000 0 -0.737114482460122 -0.865174311663682 
5500 16.9705314284761 -1.4520237724834 -1.4603416611918 
6000 36.1571850835931 -2.29359599522139 -2.3065278389124 
6500 133.792634819551 -4.66777361454465 -4.70834955863442 
7000 322.18181169659 -7.04195123386791 -7.06130780826709 
7500 203.829789185476 -7.16812176086817 -7.21857514632182 
8000 205.420563716693 -8.63533442734315 -8.64191060572781 
8500 412.331879361623 -12.3984916183681 -12.3660943814773 
9000 673.030184823405 -16.161648809393 -16.1584774389051 
9500 997.788973053588 -19.6245539312066 -19.5124839836426 
10000 1008.39457832345 -21.9915146434067 -22.2973839351374 
10500 1184.72701129473 -24.3584753556068 -24.796543430767 
11000 1498.06936475527 -26.725436067807 -27.0588280487073 
11500 2009.61421326005 -29.1371138801307 -28.9038836107455 
12000 2722.26364238704 -31.5076851550556 -30.1452376295781 
12500 2287.52815984916 -31.1403033856382 -30.6218612529492 
13000 2035.91209091406 -30.634562817686 -30.4293748200482 
13500 1586.63072146761 -29.3579612008566 -29.7343179035273 
14000 1348.8075997155 -28.2628543131522 -28.8269413765757 
14500 1413.91513562293 -27.6912600182527 -27.9722952471892 
15000 1494.84922436468 -27.1196657233532 -27.1734159286829 
15500 1574.69365732738 -26.4488499644341 -26.2765926526726 
16000 1553.08461437678 -25.3859450612425 -25.0979805557703 
16500 1248.37122646425 -23.5052774319269 -23.5290093811951 
17000 1049.5448268403 -21.6246098026112 -21.6999594239911 
17500 881.487030131652 -19.7439421732956 -19.8461688713164 
18000 835.021436366996 -18.2039449878781 -18.2014581094479 
18500 774.462598523101 -16.7816409844282 -16.765081129771 
19000 705.317410051723 -15.474531712738 -15.4839956083783 
19500 672.090247223176 -14.3643439372883 -14.3515344565155 
20000 615.589629438874 -13.277647238518 -13.2912204354939 
20500 584.905318243257 -12.2667150710887 -12.2761465339611 
21000 549.937980661359 -11.1312705806165 -11.1320559619699 
21500 468.581167115922 -9.50306530310009 -9.47896306489736 
22000 256.588158983577 -6.897276610137 -6.90970583985583 
22500 132.395577741757 -4.29148791717391 -4.29032579524572 
23000 34.3836710666841 -1.92982633962782 -1.93100419361711 
23500 4.27919806089882 -0.905302319995194 -0.906293243769078 
24000 0 -0.137586632295369 -0.608945527894223 
24500 0 0.0439502418050779 -0.482141041610555

[Top]

Plotting the output using gnuplot

profile1-bott.gnu

 
# to run type: gnuplot profile1-bott.gnu
# on the command line
reset

set terminal pngcairo  enhanced font "arial,10" fontscale 1.0 size 600, 500 
set output 'profile1-bott.png'
set multiplot layout 2,1

# Axes label
set ylabel 'Gravity (mgal)'

# Axes ranges
set xrange [0:25000]
set yrange [-40:20]

# Axes tics
set xtics 5000
set ytics 10
set title 'Gravity Profile'
plot 'profile1-bott.dat' u 1:4 w p lt rgb 'red' t 'calculated',\
     'profile1-bott.dat' u 1:3 w l lt rgb 'blue' t 'observed'
      
set xlabel 'Horizontal distance (m)'
set ylabel 'Depth (m)'
set yrange [3000:0]
set ytics 500
set title 'Sedimentary Basin Depth'
plot  "profile1-bott.dat" u 1:2 w l lt rgb 'red' notitle

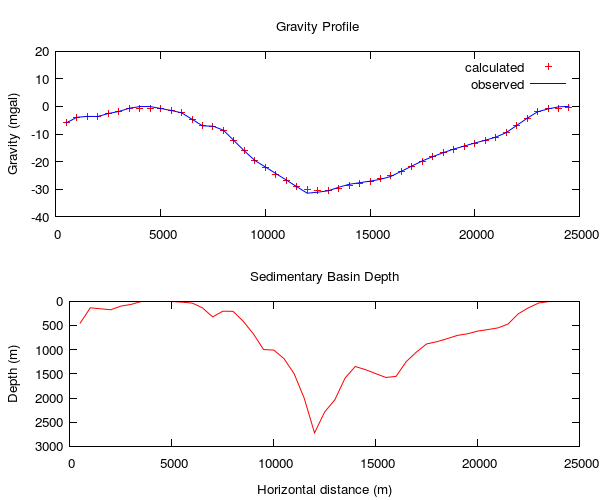
The output of the gnuplot script is shown below. The top plot shows observed gravity data (blue) and calculated gravity values (red) using a density contrast of $-500$ kg m$^{-3}$. The best-fit basin geometry after 10 iterations is shown in the bottom plot (note the vertical exaggeration).

[Top]

Some References

Bott, M.H.P., 1960. The use of rapid digital computing methods for direct gravity interpretation of sedimentary basins. Geophysical Journal International, 3(1), pp.63-67.
Telford, W.M., Geldart, L.P. and Sheriff, R.E. (1990) Applied Geophysics, Cambridge University Press.
Blakely, R. J., 1996, Potential Theory in Gravity and Magnetic Applications, Cambridge University Press

Citation
Connor, C. B. (2020) Functions for calculation of the 2d anomaly of a sedimentary basin using the Bouguer slab iteration method developed by M. Bott. Reference: https://gscommunitycodes.usf.edu/geoscicommunitycodes/public/geophysics/Gravity/bott.php

Gravity Anomaly Over a Sedimentary Basin

Use Bott's method to model gravity data measured across a sedimentary basin

Contents

Introduction

Mathematical model and Bott's iterative method

Model assumptions

Calculate the gravity using perl

Plotting the output using gnuplot

Some References

Citation